Goals
Upon successful completion of this lab, you should be able to understand and write programs using while (indefinite) loops.
Setup and Practice
Setup
- If your lab machine was not started in MacOS when you went to use it, reboot it to MacOS.
- Follow these procedures to mount your blue home-directory on the local machine and create a PyCharm project (call it Lab06). You will use PyCharm in the next part, but, it is important that you set up your project now so that if you run into any issue, we can resolve them quickly.
Practice
Answer Questions 1–7 in your Moodle writeup. You can use the the Online Python 3 tutor to help, but you should try to answer the questions on your own first.
Introduction to while loops
Enter the following Python code into the Online Python Tutor, and use the tutor to step through this loop to understand what is happening:
counter = 1 total = 0 while counter <= 5: total += counter counter += 1 print('Done')- Aswer Questions 8–10 in Moodle about the above code.
Part A: Basic while loops: the Collatz sequence
For this part of the lab, you will begin with a program that asks the user to enter a sequence of values and tells the user if each value is even or odd. You will then modify that program to do a more complex task: to generate the terms of a famous numerical sequence, called the Collatz sequence.
- Collatz Sequence
- The Collatz sequence works as follows:
- Start by choosing a positive integer N
- If N is 1, stop.
- Otherwise, based on the value of N, generate the next term:
- If N is odd, the next term is 3N+1.
- If N is even, the next term is N / 2.
- Repeat with the new value of N.
Review the above steps for how the Collatz sequence is produced, working through the following example, where the initial value for N is 6:
6, 3, 10, 5, 16, 8, 4, 2, 1
Make sure you understand the mechanics of how the above output was generated, given the starting value of 6.
- Answer Question 11 in your writeup.
Fun fact: it has not been mathematically proven that the Collatz sequence will always reach 1 and terminate. However, no one has yet found a value of N that fails to eventually reach 1. The Collatz conjecture states the unproven belief that every sequence ends in 1. The comic xkcd humorously summarizes this conjecture as:

- Create a new Python source code file named lab06a.py, substituting your name for the italicized text:
''' Program: CS 115 Lab 6a Author: Your name Description: This program will ask the user for a value and tell the user whether the value is even or odd. ''' def main(): N = int(input('Enter a number: ')) if N % 2 == 1: print(N, 'is odd.') else: print(N, 'is even.') main() - Run your program using various input values, and be sure that it accurately reports whether the user's inputs are even or odd.
- Modify this code, to begin computing the Collatz sequence, per the below pseudocode:
if N % 2 == 1: # TODO: Compute the next term in the Collatz sequence for odd N, # and set N to that value. else: # TODO: Compute the next term in the Collatz sequence for even N, # and set N to that value. # TODO: Print the new value of N.Note: you should use integer division (
//) instead of floating-point division (/) so that the values appear as integers.For example:
Enter a number: 8 The next term is 4.
or:Enter a number: 3 The next term is 10.
- To generate all the terms in the sequence, you will need a
whileloop. To practice while loop conditions, answer Question 12 in your writeup. - Put your if/else statements and your print statement inside a
whileloop:while ...: if ... else ... print ...The
whileloop condition should evaluate toTrueuntil you have finished the sequence, and then it should becomeFalse. Remember that the sequence ends when N reaches 1. The condition does not need to be long and involved — it can be very short.Note: If you accidentally write an infinite loop, you can press Ctrl-C to force-quit your program.
- Test your program using the following sample input/output sequences:
Enter a number: 8 The next term is 4. The next term is 2. The next term is 1.
Enter a number: 6 The next term is 3. The next term is 10. The next term is 5. The next term is 16. The next term is 8. The next term is 4. The next term is 2. The next term is 1.
- Demo.
When your code is correct, call an instructor over to demo your program.
Note: This week, you will demo Parts A and C, but you will only submit your Part C code. Computing the Collatz sequence was just a simple, non-trivial task to practice using a while loop.
- Continue to Part B.
- Create a new Python source code file named lab06b.py:
""" Program: CS 115 Lab 6b Author: Your name Description: This program will read a positive integer and find the largest power of two that is less than or equal to it. """ def main(): # TODO: Complete this code # Read user's input and store it as an integer in a variable called i_num. # Initialize a variable n to serve as the exponent. # Initialize a variable two_to_n to hold the value of 2**n # complete the while-loop # while two_to_n is less than i_num: # add 1 to n # multiply two_to_n by 2 # if two_to_n is greater than i_num: # subtract 1 from n # divide two_to_n by 2 # Print the result main()Read the above pseudo-code carefully, and decide on an appropriate initial value for
n. This will also determine the initial value oftwo_to_n. - Before you write any code, answer Question 13 in your writeup.
This question asks you to trace the values of
nandtwo_to_nas the program processes the input 17. Just reason using pen and paper right now. After you understand the algorithm on paper, write the Python code to replace the pseudocode. To help you test your program, here are some example input/output sequences:
- Example 1
-
Enter a number: 1 2**0
- Example 2
-
Enter a number: 67 2**6
- Example 3
-
Enter a number: 127 2**6
- Example 4
-
Enter a number: 128 2**7
- Example 5
-
Enter a number: 129 2**7
- When your program matches all of these examples, continue to Part C.
Create a new Python source file named lab06c.py:
""" Program: CS 115 Lab 6c Author: Your name Description: This program will read a positive integer and express it as the sum of powers of 2. """ def main(): # Read user's input and store it as an integer in a variable called i_num. # Outer loop: # while i_num is larger than zero: # Initialize n and two_to_n. # Do all the stuff you were doing before to find n and two_to_n. # Remember that two_to_n is the largest power of 2 less than i_num. i_num = i_num - two_to_n # print 2**n print() main()Before you translate the pseudocode to Python, answer Question 14 in your writeup. This question asks you to trace this algorithm for each iteration of the outer loop, assuming user input
i_numis 23.Once you have understood the algorithm, translate it to Python. If you need help adapting code from Part B, ask an instructor.
At this point, test your program on the following sample input:
Enter a number: 1234 2**10 2**7 2**6 2**4 2**1
There are two major changes left to make, which the rest of these steps will walk you through:
- All of the powers of 2 need to print on the same line.
- The printed terms should be separated by ' + '.
First, to have all of these values print on the same line, add
end=""to the end of your print statement. For example:print('example', end="")Now, your program is probably printing the following:
Enter a number: 1234 2**102**72**62**42**1
Next, you should add spaces and plus signs between the terms by inserting this print statement somewhere in your code:
print(' + ', end="")Now, your program should be printing the following:
Enter a number: 1234 2**10 + 2**7 + 2**6 + 2**4 + 2**1 +
You should figure out how to get rid of the final '
+' at the end. Hint: put your print statement inside some conditional statement.When you succeed, your output should look like this:
Enter a number: 1234 2**10 + 2**7 + 2**6 + 2**4 + 2**1
Demo. When you program matches the final, target behavior, demo your program for an instructor.
- Make sure that your docstring is up-to-date.
- Continue to the next part to submit your program.
- Answer the last question (#15) in your Moodle writeup. Review your answers, and then click the "Next" button at the bottom of the quiz. Once you do that, you should see a "Summary of Attempt" screen.
- Click the "Submit all and finish" button.
Warning: You must hit "Submit all and finish" so that your writeup can be graded! It is not submitted until you do this.
Once you have submitted your quiz, you should see something similar to this at the top of your Moodle window. The important part is that the State shows up as Finished.
Please leave this tab open in your browser. - Click on the "Lab 6 code" link in Moodle and open in a new tab. Follow the instructions to upload your source code (lab06c.py) for Lab06. You could either browse for your code or, using a finder window, drag and drop your lab06c.py from your cs115/Lab06 folder to Moodle. You should subsequently see a dialog box which indicates 'Submission Status' as 'Submitted for grading'. Leave this tab open in your browser.
- With these confirmation pages open in your browser, you may call an instructor over to verify that you have completed every part of the lab. Otherwise, you are done!
You will write a program that allows the user to choose the value of N, and we will generate all the subsequent terms of the sequence.
Instructions
Part B: Find the largest power of 2 less than a number
Any positive integer can be written as the sum of a series of terms, where each term is the number 2 raised to some power. For example:
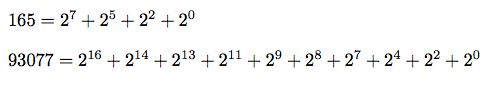
Notice how the exponent of each term is less than that of its predecessor.
You will write a program to read an integer and decompose it into such a series. Here is an example of how your final program might be used:
Enter a number: 1234 2**10 + 2**7 + 2**6 + 2**4 + 2**1
You will write your program in two phases: the first in Part B, and the second in Part C.
In the Part B phase, your program only reads an integer i_num and finds the largest n such that 2n ≤ i_num. You can assume that i_num is always a positive integer. Here is how your program will interact with the user by the end of this phase:
Enter a number: 1234 2**10
Note that 210 is 1024, and 211 is 2048. The user's number, 1234, lies in between these two values. Therefore, 10 is the largest positive integer such that 2n ≤ i_num.
Here are a few more examples:
Enter a number: 165 2**7
Enter a number: 93077 2**16
Enter a number: 1 2**0
Instructions
Part C: Write a number as the sum of powers of 2
This is the second phase, where you complete the full program described in Part B to express a positive integer as the sum of powers of 2.
Enter a number: 1234 2**10 + 2**7 + 2**6 + 2**4 + 2**1
Read the instructions carefully, and be sure you understand what you are doing at each step. Ask the lab instructors for help if you need it.