Program Correctness and Program Testing

Introduction

We begin with a short program and simple question: Is the following program correct?

   /* a simple C program */
   #include <stdio.h>
   
   /* Declare conversion constant */
   /* const tells C compiler this variable may not be changed */
   const float CONVERSION_FACTOR = (float) 1.056710;   /*quarts to liters */
   
   int main()
   {
     /* input */
     float quarts, liters;
     printf ("Enter a value:  ");
     scanf ("%f", &quarts);
   
     /* process value read */
     liters = quarts / CONVERSION_FACTOR;
   
     /* output */
     printf ("Result: %f quarts = %f liters\n", quarts, liters);
   
     return 0;
   }

The answer is "Maybe — the program may or may not be correct"; to expand, the correctness of this program depends upon what problem is to be solved.

The program is correct, IF

• one is trying to convert a value in quarts to the corresponding value of liters, AND
• float data type has adequate precision.

However, the program is incorrect otherwise:

• The program likely is not correct if we want 25 digits of accuracy in the answer.
• The program certainly is not correct if the problem was to determine whether or not it will rain tomorrow.

Point: Discussions about problem solving and the correction of solutions depend upon a careful specification of the problem.

Pre- and Post-Conditions (review)

In order to solve any problem, the first step always should be to develop a clear statement of what initial information may be available and what results are wanted. For complex problems, this problem clarification may require extensive research, ending in a detailed document of requirements. (I know of one commercial product, for example, where the requirements documents filled 3 dozen notebooks and occupied about 6 feet of shelf space.) Even for simple problems, we need to know what is expected.

Within the context of introductory courses, assignments often give reasonably complete statements of the problems under consideration, and a student may not need to devote much time to determining just what needs to be done. In real applications, however, software developers may spend considerable time and energy working to understand the various activities that must be integrated into an overall package and to explore the needed capabilities.

Once an overall problem is clarified, a natural approach in Scheme or C programming is to divide the work into various segments — often involving multiple procedures or functions. For each code segment, procedure, or function, we need to understand the nature of the information we will be given at the start and what is required of our final results. Conditions upon initial data and final results are called pre-conditions and post-conditions, respectively.

• Pre-Conditions are constraints on the types or values of its arguments.

• Post-conditions specify what should be true at the end of a procedure. In Scheme or C, a post-condition typically is a statement of what a procedure should return.

More generally, an assertion is a statement about variables at a specified point in processing. Thus, a pre-condition is an assertion about variable values at the start of processing, and a post-condition is an assertion at the end of a code segment.

It is good programming style to state the pre- and post-conditions for each procedure or function as comments.

Pre- and Post-Conditions as a Contract

One can think of pre- and post-conditions as a type of contract between the developer of a code segment or function and the user of that function.

• The user of a function is obligated to meet a function's pre-conditions when calling the function.
• Assuming the pre-conditions of a function are met, the developer is obligated to perform processing that will produce the specified post-conditions.

As with a contract, pre- and post-conditions also have implications concerning who to blame if something goes wrong.

• The developer of a function should be able to assume that pre-conditions are met.
• If the user of a function fails to satisfy one or more of its pre-conditions, the developer of a function has no obligations whatsoever — the developer is blameless if the function crashes or returns incorrect results.
• If the user meets the pre-conditions, then any errors in processing or in the function's result are the sole fault of the developer.

Example: The Bisection Method

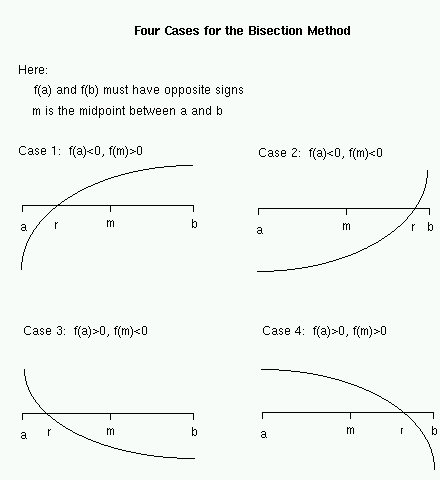
Suppose we are given a continuous function f, and we want to approximate a value r where f(r)=0. While this can be a difficult problem in general, suppose that we can guess two points a and b (perhaps from a graph) where f(a) and f(b) have opposite signs. The figure (right) shows four possible cases.

We are given a and b for which f(a) and f(b) have opposite signs. Thus, we can infer that a root r must lie in the interval [a, b]. In one step, we can cut this interval in half as follows. If f(a) and f(m) have opposite signs, then r must lie in the interval [a, m]; otherwise, r must lie in the interval [m, b].

Finding Square Roots

As a special case, consider the function f(x) = x² - a. A root of this function occurs when a = x², or x = sqrt(a). Thus, we can use the above algorithm to compute the square root of a non-negative number. A simple program using this bisection method follows:

   /* Bisection Method for Finding the Square Root of a Positive Number */

   #include <stdio.h>

   int main () {
     /*  pre-conditions:  t will be a positive number
      * post-conditions:  code will print an approximation of the square root of t
      */
   
     double t;        /* we approximate the square root of this number */
     double a, b, m;  /* the desired root will be in interval [a,b] with midpoint m */
     double fa, fb, fm;  /* for f(x) = x^2 - t, the values f(a), f(b), f(m), resp. */
     double accuracy = 0.0001;  /* desired accuracy of result */
     
     /* Getting started */
     printf ("Program to compute a square root\n");
     printf ("Enter positive number: ");
     scanf ("%lf", &t);
   
     /* set up initial interval for the bisection method */
     a = 0;
     if (t < 2.0)
       b = 2.0;
     else
       b = t;
   
     fa = a*a - t;
     fb = b*b - t;
   
     while (b - a > accuracy) {
       m = (a + b) / 2.0;  /* m is the midpoint of [a,b] */
       fm = m*m - t;
       if (fm == 0.0) break;  /* stop loop if we have the exact root */
   
       if ((fa * fm) < 0.0) { /* check if f(a) and f(m) have opposite signs */
         b = m;
         fb = fm;
       }
       else {
         a = m;
         fa = fm;
       }
     }

     printf ("The square root of %lf is approximately %lf\n", t, m);
     return 0;
   }

As this program indicates, the program assumes that we are finding the square root of a positive number: thus, a pre-condition for this code is that the data entered will be a positive number. At the end, the program prints an approximation to a square root, and this is stated as a post-condition.

A "Testing" Frame of Mind

Once we know what a program is supposed to do, we must consider how we know whether it does its job. There are two basic approaches:

• Verification: Develop a formal, mathematical proof that the program always does exactly what has been specified.
• Testing: Run the program with a range of data, in each case checking the results with what we know to be correct.

Although a very powerful and productive technique, formal verification suffers from several practical difficulties:

• We must be able to specify formally all pre- and post-conditions, and this may require extensive development.
• Formal proof techniques require extensive development and are beyond the scope of this course.
• Formal verification typically assumes that compilers are correct — as assumption that sometimes is incorrect.

Altogether, for many programs and in many environments, we often try to infer the correctness of programs through testing. However, it is only possible to test all possible cases for only the simplest programs. Even for our relatively-simple program to find square roots, we cannot practically try all possible positive, double-precision numbers as input.

Our challenge for testing, therefore, is to select test cases that have strong potential to identify any errors. The goal of testing is not to show the program is correct — there are too many possibilities. Rather, the goal of testing is to locate errors. In developing tests, we need to be creative in trying to break the code; how can we uncover an error?

Choosing Testing Cases

As we have discussed, our challenge in selecting tests for a program centers on how to locate errors. Two ways to start look at the problem specifications and at the details of the code:

• Black-Box Testing: The problem is examined to determine the logical cases that might arise. Test cases are developed without reference to details of code.

• White-Box Testing: Code is examined to determine each of the possible conditions that may arise, and tests are developed to exercise each part of the code.

A list of potential situations together with specific test data that check each of those situations is called a test plan.

A Sample Test Plan

To be more specific, let's consider how we might select test cases for the square-root function.

• Black-box Testing of the Square-Root Program

  Since we can choose any values we wish, we will choose values for which we already know the answer. Often we choose some small values and some large ones.
  • Input: 0.25 (answer should be 0.5 — (1/2)² is 1/4)
  • Input: 9 (answer should be 3)
• White-box Testing
  We want to exercise the various parts of the code.
  
  The program sets b to 2 when finding the square root of a small number, so we want to cover that case:
  • Input: 0.25 (from above — value smaller than 1)
  • Input: 1.44 (1.2 squared — value larger than 1, but smaller than 2)
  Similarly, the program sets b to t for larger numbers, and we want to cover that case:
  • Input: 9 (from above)
  The main loop stops if the loop discovers the square root exactly, so we want to select cases that have this property:
  • Input: 1 (should reach this result on the first iteration)
  • Input: 16 (should reach this result when b moves from 16 to 8 to 4)
  The main loop sometimes changes a and sometimes changes b, so we want input that guarantees we will check both of those code segments.
  • Input: 0.25 (for numbers smaller than 1, the square root is larger than the number, so a will have to move right in the loop)
  • Input: 9 (for numbers larger than 1, the square root is smaller than the number, so b will have to move left in the loop)

Putting these situations together, we seem to test the various parts of the code with these test cases:

• Input: 0.25
• Input: 1
• Input: 1.44
• Input: 9
• Input: 16

Each of these situations examines a different part of typical processing. More generally, before testing begins, we should identify different types of circumstances that might occur. Once these circumstances are determined, we should construct test data for each situation, so that our testing will cover a full range of possibilities.

Debugging

While the initial running of a program has been known to produce helpful and correct results, your past programming experience probably suggests that some errors usually arise somewhere in the problem-solving process. Specifications may be incomplete or inaccurate, algorithms may contain flaws, or the coding process may be incorrect. Edsger Dijkstra, a very distinguished computer scientist, once observed¹ that in most disciplines such difficulties are called errors or mistakes, but that in computing this terminology is usually softened, and flaws are called bugs. (It seems that people are often more willing to tolerate errors in computer programs than in other products.)²

Novice programmers sometimes approach the task of finding and correcting an error by trial and error, making successive small changes in the source code ("tweaking" it), and reloading and re-testing it after each change, without giving much thought to the probable cause of the error or to how making the change will affect its operation. This approach to debugging is ineffective, for two reasons:

• Tweaking is time-consuming. Novice programmers tend to have a naive confidence that the next small change in the source code, whatever it is, will fix the problem. This is seldom the case. If you detect an error in a procedure, and the first tweak doesn't fix it, the next twelve tweaks probably won't either -- so don't bother with them. Push yourself away from the keyboard and study the context. Don't make even one more change in the source code until you're ready to test a well-thought-out hypothesis about the cause of the error. (This is also a good time to make a separate copy of the procedure, in Emacs, so that you can backtrack to the current version if subsequent experimentation requires extensive temporary rewriting.)

• Tweaking usually fixes only a specific, local problem. Very often an error is a symptom of a general misunderstanding on the part of the programmer, one that affects the operation of the procedure in cases other than the one being tested. Unless you address this general problem, tweaking a procedure in such a way that it passes the particular test that it formerly failed is likely to make your program worse instead of better.

A much more time-efficient approach to debugging is to examine exactly what code is doing. While a variety of tools can help you analyze code, a primary technique involves carefully tracing through what a procedure is actually doing. We will discuss various approaches for code tracing and analysis throughout the semester.

Notes

1. Edsger Dijkstra, "On the Cruelty of Really Teaching Computer Science," Communications of the ACM, Volume 32, Number 12, December 1989, p. 1402.
2. Paragraph modified from Henry M. Walker, The Limits of Computing, Jones and Bartlett, 1994, p. 6.