Laboratory Exercise on Simulation and More Program Management: Functions, Value Parameters, and Assertions

Goals

This laboratory exercise provides initial practice with simulations, functions/procedures, passing values as parameters, and return values within C programs.

Introduction

A function or procedure in C is designed to perform a task. Several variations are possible, such as the following:

• The task may be self contained, or it it may depend upon some starting data.
• The task may or may not change its environment (e.g., the task might move the robot or print something to a terminal window).
• When the task finishes, data may or may not be computed and returned for use in the main program.

Altogether, a function or procedure performs some work. Variations arise in whether or not data are needed to start the work and whether or not computed results are returned to the main program.

Work Started in Class

Family-size Simulations

The readings on simulation and functions and program management present six programs that investigate the number of children a couple might expect to have, if it decides to continue having children until it has at least one boy and at least one girl.

1. Copy each of the programs, couple-1.c, couple-2.c, couple-3.c, couple-4.c, couple-5.c, couple-6.c, to your account.

   1. Compile and run each program, and review the output obtained.
   2. Explain, in your own words, the basic approach for the simulation, as implemented in couple-1.c.
   3. Write a paragraph (at least four sentences) on how each of the later versions of this simulation differ from the previous version.

2. Extend the investigation of the family-size problem for a wider range of decimal fractions for the overall proportion of boys. In particular, in program couple-6.c, the main loop

     double boy_fraction;
     for (boy_fraction = 0.5; boy_fraction <= 0.52; boy_fraction += 0.002)
       {
         simulate_several_couples (numberOfCouples, boy_fraction);
       }
   

   examined a rather narrow range of decimal fractions for boys and determined that small changes in this number had little impact on family size. Expand the range of this investigation substantially by running the program with each of these statements.

     for (boy_fraction = 0.35; boy_fraction <= 0.65; boy_fraction += 0.005)
   

   and

     for (boy_fraction = 0.25; boy_fraction <= 0.75; boy_fraction += 0.005)
   

   In each case, review the results and interpret what you see.

Rolling a Die

Since the rand() function returns a random integer between 0 and RAND_MAX, the expression rand()%6 returns a random integer between 0 and 5 (inclusive), and 1+rand()%6 returns random integers between 1 and 6. Thus, this expression can be used to simulate the rolling of a die.

3. Rolling 2's: Write a program that reads an integer N, rolls a die N times, and counts the number of times a 2 is thrown.

4. Rolling until a 2: Write a program that prints the number of rolls of a die until a 2 is thrown.

Tossing a Coin

Program coins.c, by Erik Opavsky, simulates the flipping of a coin 100 times and counts the number of times that two tails appear in consecutive tosses.

5. Copy coins.c.

   1. Compile and run the program several times to observe what it does.
   2. Write a detailed commentary that explains how the program works.
      • How does the program simulate flipping a coin? For example, what circumstance is interpreted as a head or as a tail?
      • What is the purpose of the previousFlip variable?
      • How does the program keep track of when two tails are flipped in a row?

6. Write a program that flips a coin 500 times and counts the number of times a tail is flipped immediately after a head.

void and non-void Functions

Consider the program quadratic.c that solves the quadratic formula ax² + bx + c = 0, while illustrating several common variations for simple functions.

7. Copy quadratic.c to your account, compile and run it, and review the code to determine how it works.

   1. Procedure printEqn has a void return type. Parameters are passed into printEqn, but nothing is passed back. What happens if the statement return a+b+c is inserted at the end of this procedure? (Try compiling the code and explain what happens.)

   2. Procedure printEqn is called in both procedures eqn1 and eqn2 with just a simple statement, such as:

        printEqn   (1.0, -3.0, 2.0);
      

      What happens if you try to assign the result of printEqn to a variable, such as

        double value = printEqn   (1.0, -3.0, 2.0);
      

   3. Procedure disc returns a double. Sometimes beginning coders separate the call to a function with the assignment of the return value. Here are two examples:

      Attempt 1:

        double discriminate;
        disc (a, b, c);
      

      Attempt 2:

        disc (a, b, c);
        double discriminate;
      

      Try each of these attempts within procedure printRoots.

      • Does the code compile?
      • Does the code give the desired result?

   4. Change the body of disc to the following

        printf ("r = %lf, s = %lf, t = %lf\n", r, s, t);
        return sqrt (s*s - 4*r*t);
      

      Compile and run the program
      Note: To compile a program that uses the square root function sqrt, you likely will need to add -lm to the gcc command to invoke the math library
      

      gcc -o quadratic -lm quadratic.c
      

      • Describe what is printed by the overall program. What might you conclude about what happens when printing is done in the middle of a computation? For example, how does this impact the overall program's output?
      • Can you identify any guidelines regarding the advisability of including print statements in functions designed for computation (e.g., disc)?
      • In addition to the printf statement in function disc, insert the code from Step 7c (into printRoots). What happens when procedure with a return value (e.g., disc) is called on a line by itself?

Writing Numeric Functions

8. Within a C program, define and use the following functions:

   • Function circum that takes a circle's radius as parameter and returns the circumferences of the circle.

   • Function area that takes a radius as parameter and returns the area of the circle with that radius.

Homework

Functions, Values as Parameters, and Robot Motion

9. Write a function smallestOf3 that has three double parameters and returns the smallest value from the three.

   Program yoyo-program.c uses a function yoyo to control a Scribbler 2 robot.

10. Copy the yoyo-program.c program to your account, compile and run it, and review to code to determine how it works.

    1. Explain what the program does.

       • What movements does the robot make? Why?
       • What output is printed? Why?

    2. In the main program, duplicate the line

         result = yoyo (repetitions);
       

       (I.e., this line should appear twice in succession.)

       Does making this call twice change how many times the robot yoyos in each call? Why or why not?

    3. In the main program, replace the line

         result = yoyo (repetitions);
       

       by

         repetitions = yoyo (repetitions);
         repetitions = yoyo (repetitions);
       

       Does making this call twice change how many times the robot yoyos in each call? Why or why not?

    4. In C, variables declared within a function are separate from variables declared elsewhere (e.g., in main). In the original program, change the name of the repetitions variable to reps throughout the main procedure. Compile and run the program.

       Does changing yoyo's variable reps have any impact on the variable reps in the main procedure?

    5. Again, return to the original program. This time nest the call to yoyo in the main procedure. That is, the call to yoyo will become:

       yoyo (yoyo (repetitions));
       

       • Make a prediction of what will happen with the above nested call.

       • Test out your nested call and explain what happened.

Finding Roots using the Bisection Method

Suppose we are given a continuous function f, and we want to approximate a value r where f(r)=0. (Jargon: r is called a root of the function f.) While finding r can be a difficult problem in general, suppose that we can guess two points a and b (perhaps from a graph) where f(a) and f(b) have opposite signs. If the graph crosses the x-axis at the midpoint m of the interval between a and b (i.e., if f(m)=0), then m is the desired root of the function. Otherwise, the four possible cases are shown below:

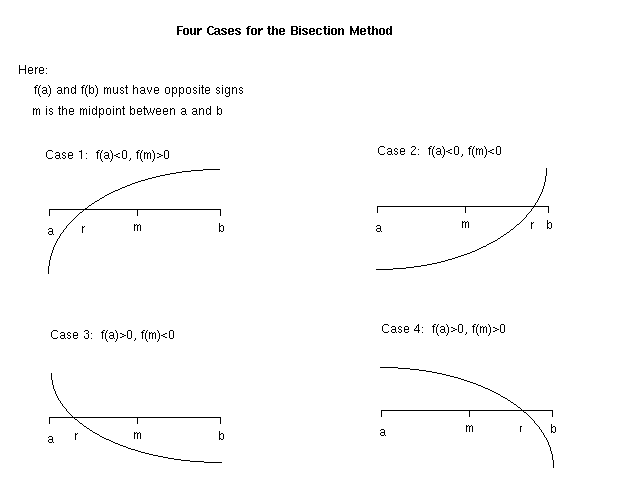
Since this setting assumes we are given a and b for which f(a) and f(b) have opposite signs, we can infer that a root r must lie in the interval [a, b]. In one step, we can cut this interval in half as follows. If f(a) and f(m) have opposite signs, then r must lie in the interval [a, m]; otherwise, r must lie in the interval [m, b].

Following this process of cutting the interval in half, we can continue until the interval is very narrow. At this stage, the midpoint of the interval will be a reasonable approximation to a root of the function.

11. Write a program that uses the Bisection Method to approximate a root of a function.

    • The start of the program should define a function

      double f (double x)
      

      for which the program is to find a root.

    • The program should define a new function

      double find_root (double a, double b, double accuracy)
      

      which works as follows:

      • find_root should use an assert statement to check that f(a) and f(b) have different signs. (The program should terminate if this assumption is not met.)
      • Another assert statement at the beginning of find_root should check that the accuracy is positive.
      • find_root should continue to cut the interval in half, following the Bisection Method, until either f(m)=0 for a computed midpoint m or the newly computed interval is shorter than the accuracy specified.
      • find_root should return the computed midpoint of the final interval.
    • The main program should ask the user to enter endpoints a and b and the accuracy. The main program then should call find_roots with the appropriate parameters and report the result.