Assignment on Topological Sorting, Partition, and Quicksort

As suggested by this assignment's title, this exercise is organized into three parts:

• topological sorting
• the partition procedure and alternative loop invariants
• quicksort, improved quicksort, and hybrid quicksort

Topological Sorting

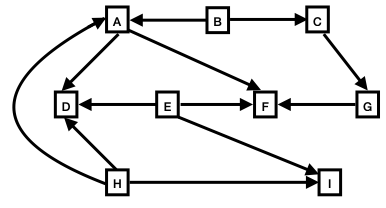
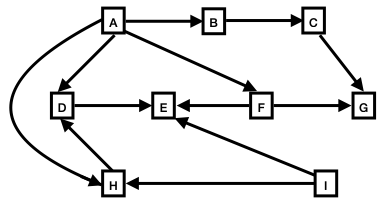
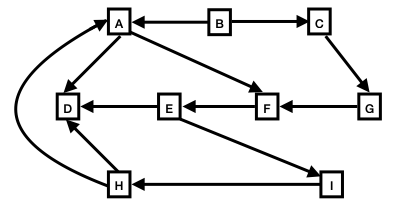
1. Consider the following directed three graphs.

   Directed Graph 1		Directed Graph 2		Directed Graph 3

   For each of these graphs, answer the following:

   • If a topological sort can be performed on this graph, show the results of the sort, and briefly explain how this result was obtained.
   • If a topological sort does not exist for this graph, explain why.

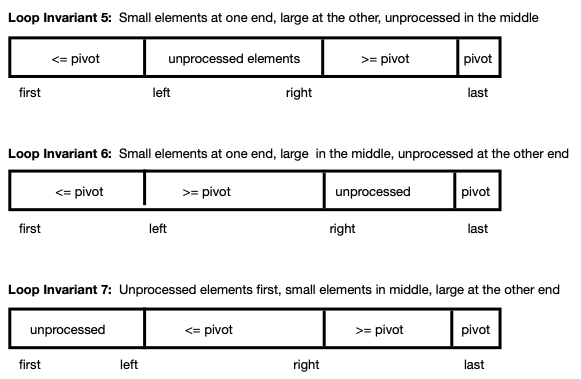
The Partition Procedure and Alternative Loop Invariants

The Reading on Quicksort discusses four possible loop invariants for the Partition Problem, each based on using the left element in an array segment as a pivot. A similar, but alternative, approach uses the right element in an array segment as a pivot. This alternative considers three additional loop invariants.

2. Based on the Reading on Quicksort, the program partitions-alt.c provides

   • two versions of partition, one based on implementation 1A, and one on based on implementation 1B
   • a framework for including and testing additional partition functions

   1. Review the program and explain

      • the purpose of the code

          typedef struct algs {
             char * name;
             int (*proc) (int [ ], int, int, int);
          } partitionType;
                    

        and how this structure is used.

      • the purpose of the line

        #define printCopyTime 0  // 1 =  print times to copy arrays; 0 = omit this output
                    

        and how printCopyTime is used.

      • what steps are involved to time segments of code in C/C++ (be sure to identify what function(s) is(are) called).

      • explain the purpose of variables, maxreps and copy_time, and why these variables are needed.

   2. Expand this program by inserting the following two functions and updating the main procedure to include them in test runs:

      • a procedure that implements Loop Invariant 5, given above
      • a procedure that implements Loop Invariant 7, also given above

      Note: Both of these procedures must be based on the Loop Invariants specified. Procedures violating the specified Loop Invariant will lose [almost] all credit for that part.

   3. After running the expanded program from Step 2, turn in a copy of the output obtained, and answer these questions.

      • Which, if any, of the implementations of the partition are most efficient? Why do you think this result is observed?
      • Roughly, how do the times change for each procedure, when the data sets double in size with each main iteration? Does this experimental timing suggest Big-O or Big-θ for the run-time? Explain.

3. Finding the kth smallest item: The partition method may be used to find the kth smallest element in an array, by narrowing the range to be examined within the overall array. For example, suppose that partition returns index middle as the location of the final location for the pivot. Basic processing involves three cases:

   • If middle is k-1, that is, if middle is the kth element in the array, then the element at that position is the kth smallest.

   • If middle < k-1, then one should look for the k smallest element in the subarray to the left of the index middle.

   • If middle > k-1, then one should look for the k smallest element in the subarray to the right of the index middle.

   Write a procedure kthSmallest to find the kth smallest element in any array. kthSmallest should use procedure partition and the above notes the above algorithm to guide its processing. Your lab write up should include the code for kthSmallest, the enclosing program used for testing, and the test runs used for checking correctness.

   Note: For an array of size n, setting k to n/2 enables kthSmallest to find the median value.

Notes on Steps 2 and 3: For Steps 2 and 3 in this assignment, you should submit:

• A complete listing of the program used for each part.
  • If the kthSmallest procedure of Step 3 is included in the program for Step 2, then one program can be turned in for the two parts.
  • If the kthSmallest procedure is written in a separate program (that implements some version of a Quicksort), then the two programs (for Step 2 and for Step 3) must be submitted.
• Output obtained for both Steps 2 and 3 must be included in your submitted work--either in a single extended output or in two separate output printouts.
• Answers to questions asked in Step 2a should be submitted as well as the program listings and output.

Quicksort, Improved Quicksort, and Hybrid Quicksort

4. Program quicksort-comparisons.c contains two copies of quicksort procedures and a framework for timing the running of these procedures on ascending, random, and descending data sets of varying sizes. In particular,

   • Functions basicQuicksort, basicQuicksortHelper, and basicPartition implement the basic quicksort algorithm.
   • Functions imprQuicksort, imprQuicksortHelper, and imprPartition begin as copies of the corresponding basic functions, and will be modified as part of this problem.

   These functions come directly from the Reading on Quicksort

   1. Revise the relevant function(s) labeled "impr", to transform the code to implement an "improved quicksort". In brief, an "improved quicksort" modifies the "basic quicksort" by selecting a random element in the array segment between index left and right, and swapping that element with the element at array index left. Otherwise, the "improved quicksort" is the same as the "basic" version.
   2. Run the program and describe what happens. Why do you think the program crashes on ascending and/or descending data for the basic quicksort, once the data set gets to a certain size?
   3. Modify the testing component of the main procedure, so that the basic quicksort component is run only for ascending or decreasing data sets of relatively small size, but times for those data sets are given only as "---" for larger data sets. The full program still should produce timing output for the basic quicksort for all sizes of random data and for the improved quicksort for all data sets. For example, part of the output might have the following format (although the numbers may be [quite] different).

                          Data Set                   Times
      Algorithm             Size     Ascending Order   Random Order  Descending Order
      basic quicksort      40000          1.1  ok        0.0  ok           1.1  ok
      improved quicksort   40000          1.1  ok        0.0  ok           1.1  ok
      
      . . .
                          
      basic quicksort     160000         18.1  ok        0.0  ok          18.0  ok
      improved quicksort  160000         17.9  ok        0.0  ok          18.0  ok
      
      basic quicksort     320000         ----            0.0  ok          ----
      improved quicksort  320000          0.0  ok        0.0  ok          0.0  ok
      
      . . .
                          
      basic quicksort    2560000         ----            0.4  ok          ----
      improved quicksort 2560000          0.2  ok        0.4  ok          0.2  ok
      
      . . .
              

   4. Review the output produced by this updated program (and turn it in with the revised program and other answers to this assignment). Under what circumstances, if any, does the improved quicksort yield better results than the basic version? Explain these results briefly, based on your program runs.

5. Expand the program in Step 4 to include a hybrid quicksort function (with any needed helper functions—perhaps copied with minor revision from the improved quicksort). The hybrid quicksort, is described in the Reading on Quicksort.

   1. The expanded program should include these elements:
      • The revised hybrid quicksort function should include another parameter—the maximum size of the array segment for an insertion sort (before the improved quicksort is used).
      • For each data set, the main program should call the hybrid quicksort with the maximum size for the insertion sort having values 4, 5, 6, . . . 11.
      • The maximum sized data set should be set as 40960000
   2. Print out the results of a sample run of this program, and answer these questions:
      • For which array-segment sizes, if any, does the insertion sort improve the performance of the hybrid quicksort?
      • What optimal size of an array segment should be used for an insertion sort, rather than a quicksort, in this hybrid algorithm? Explain briefly.

Notes on Steps 4 and 5: Since Step 5 extends Step 4,

• A single, extended program listing that contains code for the basic quicksort, improved quicksort, and hybrid quicksort.
• A single output listing for parts 4c and 5b.
• Commentary for parts 4b, 4d, and 5b.

created August 6, 2022 revised August 9, 2022 revised September 27, 2022 revised December 30, 2022 revised Summer, 2023 revised Novemver 30, 2024
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.