Assignment on Graph Basics and Singly-nested Loop Invariants
Work for this assignment falls into two groups:
Graph Basics
Adjacency Matrices and Lists
-
Consider the following adjacency matrix S for a weighted
graph. (Note: 0 means there is no edge.)
| | A | B | C
| D | E | F | G
| H
|
| A | 0 | 3 | 0 | 0 | 4 | 7 | 0 | 0
|
| B | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0
|
| C | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0
|
| D | 2 | 0 | 0 | 0 | 8 | 0 | 0 | 0
|
| E | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5
|
| F | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0
|
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7
|
| H | 0 | 8 | 0 | 5 | 0 | 0 | 0 | 0
|
-
Draw a picture of the graph represented by this adjacency matrix S, including
the weights.
-
Can this graph be interpreted as being directed? Explain.
-
Can this graph be interpreted as being undirected? Explain.
-
List the vertices in depth-first order beginning with vertex A.
When you have a choice among vertices, pick them in alphabetical
order. (For example, if at some point during the execution of the
algorithm, both vertices B and D needed to be enqueued or pushed
onto a queue or stack, respectively, then B would be
enqueued/pushed before D.)
-
List the vertices in breadth-first order beginning with vertex A.
As in Part 1d, when you have a choice among vertices, pick them in
alphabetical order.
A Graph Specified by Sets
-
Consider the following graph, specified in terms of sets of
vertices and directed edges.
- G = {V,E}
- V = {A, B, C, D, E, F, G, H, I, J}
- E = { <A, B, 1 >,
<A, D, 2 >,
<B, A, 1 >,
<B, C, 6 >,
<B, F, 3 >,
<C, B, 6 >,
<C, F, 4 >,
<C, G, 1 >,
<D, A, 2 >,
<D, E, 6 >,
<D, H, 3 >,
<E, D, 6 >,
<E, F, 1 >,
<E, I, 5 >,
<F, B, 3 >,
<F, C, 4 >,
<F, E, 1 >,
<F, I, 6 >,
<F, J, 5 >,
<G, C, 1 >,
<G, J, 2 >,
<H, D, 3 >,
<H, I, 8 >,
<I, E, 5 >,
<I, F, 6 >,
<I, H, 8 >,
<I, J, 7 >,
<J, F, 5 >,
<J, G, 2 >,
<J, I, 7 >
}
-
Write the adjacency matrix for this graph, based upon the
alphabetical ordering of the vertices given.
-
Draw the adjacency list representation for this graph.
-
Can this graph be interpreted as being directed? Explain.
-
Can this graph be interpreted as being undirected? Explain.
-
List the vertices in depth-first order beginning with
vertex A. As in Problem 1, when you have a choice among
vertices, pick them in alphabetical order.
-
List the vertices in breadth-first order beginning with vertex
A. As in Problem 1, when you have a choice among vertices,
pick them in alphabetical order.
Analytical/Structural Results
-
Suppose a connected graph has v vertices and e edges. What is the complexity of
a breadth-first search?
-
Assume the queue is implemented with an array, and the graph by an
adjacency matrix.
-
Assume the queue is implemented with a linked list, and the graph with
adjacency lists.
Invariants for Singly-nested Loops
In this section, you are asked to write three programs, all
involving loop invariants for singly-nested loops. Of course, all
programs must follow the C/C++ Style Guide!
Binary Search Algorithms
-
The Reading
on an Introduction to Loop Invariants discusses two implementations
of a binary search, based on different loop invariants, and
program binary-searches.c
provides the full code for each of these invariants, as well as a
framework for testing these functions.
The reading identifies two variations for the desired result of
a binary search:
-
Return true or false according to whether or not the
item is present.
-
Return the array index where value is found, or return the index of the
first array value larger than the item. (If item is
larger than all items in the array, return the array size — the
index after the last array element.)
Following the second variation as the desired result,
expand binary-searches.c to include a new
function search3 that implements and tests a binary
search that uses the following loop invariant.
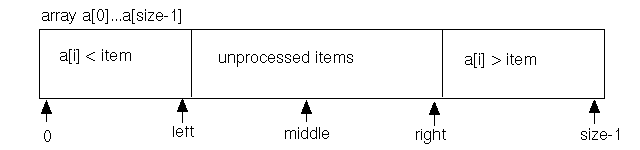
To clarify both the processing and the desired results,
left is the largest array index for which it is
known that a[left] < item (provided some
elements are known to be less than item, or equivalently
left is the first index for
which a[left+1] is unprocessed (provided some
elements have not yet been examined).
right is the largest array index for
which a[right] is unprocessed (provided some
elements have not yet been examined), or equivalently
right is the first index .for which it is
known that a[right+1] > item (provided some
elements are known to be larger than item
- the valued returned by the function should be as follows:
- if the desired value is found in the array, the index
of the element should be returned. (If the desired value
appears several times in the array, then the index of any
of those repeated values may be returned.)
- if the desired value is not found, then the search
should return the following:
- if the desired value is smaller than at least
one array element, then the index of the first element in the
array larger than the desired value should be returned.
- if the desired value is larger than all elements
in the array, then the size of the array should be
returned.
To clarify the required return value, consider the following
array of 13 elements:
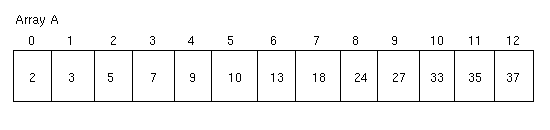
-
If the array is searched for the number 7, then index 3 is
returned.
-
If the array is searched for the number 8, then the index 4 is
returned (the value 9 in the array is the first value bigger
than 8, so its index is returned.
-
If the array is searched for the number 39, then the size of the
array (13) is returned, as all elements in the array are
smaller than 39.
The Dutch National Flag Problem
The Dutch National Flag Problem was first proposed by W.H.J. Feijen and
made famous by Edsger W. Dijkstra. The following formulation relates the
problem to arrays in C.
Enumerations in C are described in Kernighan and Ritchie, Section 2.3,
page 39. For example, an enumeration with three colors could be declared
as:
enum color { red, white, blue };
and we may consider an array of colors:
#define size 50 /* number of elements in an array */
color colors [size];

When we begin, we do not know the number of elements of each color, and we
are not even assured that each color is actually present.
The Dutch National Flag Problem seeks to sort this array, so that red's
come first, then white's, and then blue's. Movement of array elements may
be accomplished only by swapping two items.

Solution
Although one approach to this problem involves simple sorting (just
consider red < white < blue), the problem can be solved in a single
pass of the data. The idea is to identify an array diagram that describes
sections of colors as loop invariants. Writing the code then is reasonably
straightforward; we just have to maintain the invariant!
For this problem, at least four different pictorial loop invariants
initially come to mind:

In each case, one must introduce variables to keep track of the edge of the
red, white, and blue sections. Initially, these sections contain no
elements, and the entire array is unprocessed. Then as processing
proceeds, the program looks at successive unprocessed elements and puts
them in their correct locations — maintaining the loop invariant.
-
Write a complete program to solve this problem, using either
Invariant A or Invariant D.
-
For your chosen invariant, initialize your variables, so that the
pictorial loop invariants are satisfied at the start of processing.
-
Complete the loop processing, maintaining the identified loop invariant.
-
Once code segment for the Dutch National Flag Problem is
written, place it within a complete program, so you
can test that your code works properly.
-
In submitting your work for this problem, include both the
complete program and sample test runs.
-
Of course, as with any program for this course, the code must
follow the course's C/C++ Style Guide.
-
Repeat Exercise 5, choosing either Invariant B or Invariant C.
created August 7, 2022
revised August 9, 2022
revised December 29, 2022-January 2, 2023
minor editing February 15 and 22, 2023
minor editing Summer, 2023
|


|
|
For more information, please contact
Henry M. Walker at
walker@cs.grinnell.edu.
|





