| CS 415, Section 001 | Sonoma State University | Spring, 2024 |
|
Algorithm Analysis
|
||
|
Instructor: Henry M. Walker
Lecturer, Sonoma State University | ||
Although much of this course has been well developed in recent semesters, the SSU CS faculty recently have approved a partially-updated course description. Currenly, the Web site is reasonably stable, but modest refinements are possbile.
Since May, 2024, the California Faculty Association (CFA) – the labor union of professors, lecturers, librarians, counselors, and coaches across the 23 California State University campuses – has been in negotiations with the management of the California State University System. After a one-day strike on Monday, January 22, the two sides have reached a tentative agreement, and the strike has been called off. Effective Tuesday, January 23, SSU classes (including CS 415) will be held as scheduled.
To introduce the concept of loop invariants within the context of singly-nested loops, this reading is organized into two parts:
A Simple Problem: Consider the task of reading a (nonzero) number r from a terminal window and printing r0, r1, r2, r3, ..., r10.
Program loop-invariants-1.c
demonstrates that even this simple problem can have three different,
but correct, solutions. The following code segments
assume r has already been read.
// Solution 1 // Solution 2 // Solution 3
prod = 1; printf ("\t%6.2lf", 1.0); printf ("\t%6.2lf", 1.0);
i = 0; prod = 1 prod = r;
while (i <= 10) { i = 0; printf ("\t%6.2lf", prod);
printf ("\t%6.2lf", prod); do { i = 0;
prod *= r; i++ while (i < 9) {
i++; prod *= r; i++;
} printf ("\t%6.2lf", prod); prod *= r;
printf("\n"); } printf ("\t%6.2lf", prod);
while (i < 10); }
printf("\n"); printf ("\n");
Although each of these solutions print the proper output, the
initializations of i, the type of loop differs, the
order of statements within the loop varies, and the condition for
the loop to continue varies.
The underlying issue for program development is that the
variable i and prod have somewhat
different relationships with each other and to the output. Since
these relationships evolve during the loop, we articulate these
relationship at the top of a loop (when the while
or do is encountered.
| // Solution 1 | // Solution 2 | // Solution 3 |
| prod == ri | prod == ri | prod == ri+1 |
| powers through ri-1 printed | powers through ri printed | powers through ri+1 printed |
| it always true that 0 <= i <=11 | it always true that 0 <= i <=10 | it always true that 0 <= i <=9 |
In the while statements, the conditions (i
<=10), (i <10), and (i
<9), are sometimes called continue conditions; each
loop continues as long as the condition is true. In contrast, the
negation of each expression, (i >10), (i
>=10), and (i >=9), are sometimes
called exit conditions; program execution leaves the
beginning/end of the loop when the condition is false.
In contrast, each relationship above is always true, and is called a loop invariant.
assert ((0 <= i) && (i <= 11));
prod = ru).
powers
through ri-1 printed?)
The point here is that even code for a simple problem can be
approached in multiple ways, but code for one approach may not be
interchangeable with code from another approach. Further, in
isolation, a statement (e.g., prod = r) may look quite
reasonable, but it may not fit properly with other parts of the
code.
Although trial and error is one way to get all parts of a code segment to work together properly, writing out loop invariants initially is an important technique to clarify relationships and write code properly the first time.
Common, but Important, Observation for Code Development:
Hours of coding can save minuts of initial analysis and design!.
In developing a loop:
The binary search involves looking for an item within an array that has already been sorted. We begin with an array of data a[0], ..., a[size-1], and we wish to search for a particular item. The approach is to look for item in the middle of the array and make inferences about where to look next. Overall, the binary search allows us to divide the amount of data under consideration in half each time.
To understand how this is done, we consider how we might look up a name in a telephone book. We begin by opening the telephone book to the middle. If we are lucky, we see the name on the page in front of us. However, even if we are unlucky, we can tell which half of the book contains the name.
Once we know which half the name is in, we turn to the middle of that half. Again, we might be lucky and find the name immediately. Otherwise, we can restrict our attention to just that part where the name must be. (We are now looking at just one-quarter of the original book.)
As we proceed in subsequent steps, we continue looking at the middle page of the section remaining, and dividing that section in halves until we find the name or until we run out of pages to look at.
Before developing code, we must clarify what result we might want when we are done. Here are two of the various possibilities:
Here, we ask for the second result. In practice, if data are in the first part of a large array, then the index returned will indicate where to insert a new item, so the array will remain ordered; we would just slide larger elements to the right within the large array and insert the new item.
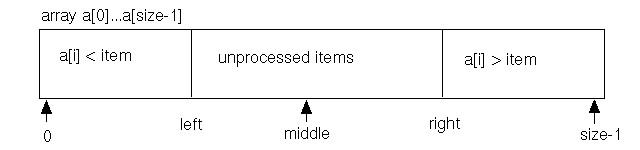
To describe processing, we first translate the algorithm to a general picture:

In this picture, array elements on the left of the array have been determined to be smaller than the desired item, and elements on the right have been determined to be larger. The variables left and right mark the boundaries of these checked regions, and middle marks the location halfway between left and right.
Although this high-level picture presents a useful vision for the algorithm, three details require clarification:
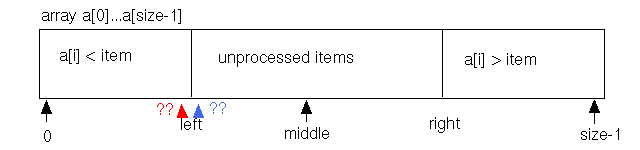
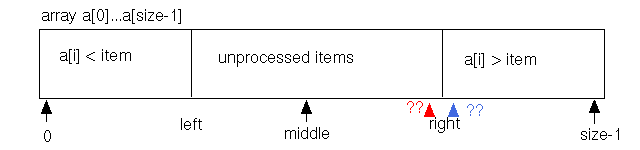
If there are an odd number of items remaining unchecked, then middle can indicate exactly the middle array element to be checked. However, if there are an even number of items, should middle be rounded up or down? In C/C++, the two likely computations are:
middle = (left + right) / 2; /* when dealing with integers, C/C++ rounds down */ middle = (left+right+1) / 2; /* adding 1 ensures rounding up in C/C++ */
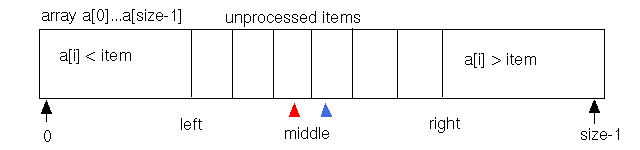
For example, the following figure shows six unprocessed elements, so middle may be either the third or fourth element in the array segment.
In practice in coding, any combination of the above choices can lead to correct code, but consistency is essential. When the meanings or interpretation of variables changes within the code, the code likely fails — at least in some cases, and fixing the identified errors often creates new ones.
Although each interpretation of left, middle, and right can be specified precisely in words, use of a picture can capture the key elements easily and quickly. Such an approach is called a pictorial loop invariant. As an illustration, we
choose one variation of assignments from above and develop the code. Then,
to show other choices also might work, we choose a different variation and
develop code for that as well.
In this variation, we choose left and right to be the unprocessed items next to the boundary; we defer the choice of computation for middle until later.
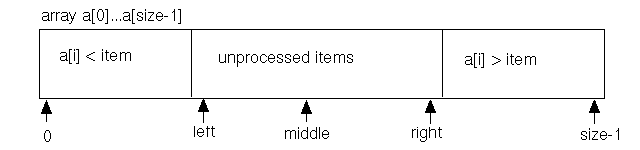
With this choice of loop invariant, we initialize left and right to the extreme ends of the array which have not been processed:
left = 0; right = size - 1; middle = ??? /* one of the computations above, does it matter? */
When we consider a guard for our loop, we need to decide when to continue and when to exit. To determine the right conditions, we extend our picture of the loop invariant to when the unprocessed area has shrunk to nothing:
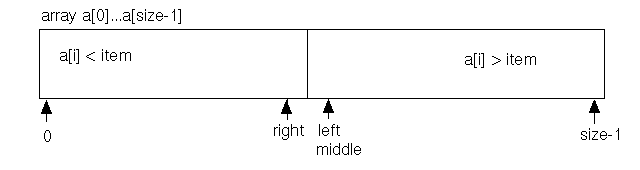
At first, this diagram may seem peculiar — left and right have moved past each other, but let's examine this carefully.
Translating this picture into C/C++ code, we first identify the needed condition for continuing the loop. We only stop when right < left or when we have found the desired item, so the main loop should begin:
while ((left <= right) && (a[middle] != item)) {
Within the loop, we will compare a[middle] with item and update either left or right, but what should the update value be? In order to maintain the loop invariant, we need to change the left or right variable to an unprocessed value, and we have already checked a[middle]. Thus, we should move up or down from middle in our assignment:
if (a[middle] < item)
left = middle + 1;
else
right = middle - 1;
Finally, what about the computation of middle? We have already noted that at the end we want middle == left. Also, from the picture, we know that at the end left = right + 1. Let's try these values for left or right in the two computations above:
Rounding down:
middle = (left + right) / 2;
= (right + 1 + right) / 2 /* substitution */
= (2*right + 1) / 2
= right + 1/2
= right /* C's integer division rounds down */
Rounding up:
middle = (left + right + 1) / 2;
= (right + 1 + right + 1) / 2 /* substitution */
= (2*right + 2) / 2
= right + 2/2
= right + 1
= left
This shows that if we round up, middle will have the needed value, but if we round down, our computation will be off by one.
Putting all the pieces together, we get the following code based on this loop invariant:
/* Binary Search, Version 1 */
left = 0;
right = size - 1;
middle = (left + right + 1) / 2; /* we must round up */
while ((left <= right) && (a[middle] != item)) {
if (a[middle] < item)
left = middle + 1;
else
right = middle - 1;
middle = (left + right + 1) / 2;
}
As we have discussed, middle is the index where either a[middle] == item or middle is the place to insert item to keep the array elements ordered.
In this variation, we choose left as in version 1, but we choose right to be the examined element closest to the boundary; as before, we defer the choice of computation for middle until later.
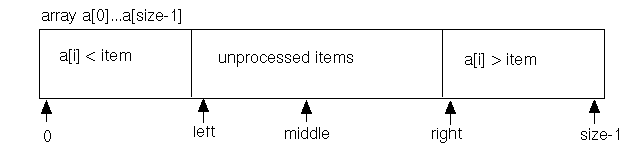
With this choice of loop invariant, we initialize left to the
extreme left end of the array which have not been processed, but we must
initialize right to just to the right of the array—initializing right to size-1 would imply that we already have determined a[size-1] > item. Again, we
leave computation of middle until later.
left = 0; right = size; middle = ??? /* one of the computations above, does it matter? */
When we consider a guard for our loop, we need to decide when to continue and when to exit. To determine the right conditions, we extend our picture of the loop invariant to when the unprocessed area has shrunk to nothing:
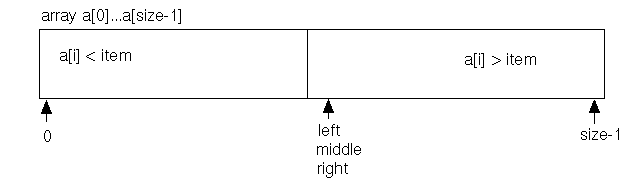
In this case, left, middle, and right all come together just after the small elements, and they designate the first large element. Again we look at the diagram carefully:
Translating this picture into C/C++ code, we first identify the needed condition for continuing the loop. We only stop when right == left or when we have found the desired item, so the main loop should begin:
while ((left < right) && (a[middle] != item)) {
Within the loop, we will compare a[middle] with item and update either left or right, but what should the update value be? In order to maintain the loop invariant, we need to change the left variable to an unprocessed value, but we should change right a processed one. In either case, we have already checked a[middle]. This gives rise to the following assignments:
if (a[middle] < item)
left = middle + 1;
else
right = middle;
Finally, what about the computation of middle? We have already noted that at the end we want middle == left == right. Let's try these these values for left or right in the two computations above:
Rounding down:
middle = (left + right) / 2;
= (right + right) / 2 /* substitution */
= (2*right) / 2
= right /* C's integer division rounds down */
Rounding up:
middle = (left + right + 1) / 2;
= (right + right + 1) / 2 /* substitution */
= (2*right + 1) / 2
= right + 1/2
= right /* C's integer division rounds down */
This shows that we will get the same result whether we round up or down, so the choice of rounding does not seem to matter. Typically, we round down because it seems a bit simpler.
Putting all the pieces together, we get the following code based on this loop invariant:
/* Binary Search, Version 2 */
left = 0;
right = size;
middle = (left + right) / 2; /* rounding does not matter here, so we round down for simplicity */
while ((left < right) && (a[middle] != item)) {
if (a[middle] < item)
left = middle + 1;
else
right = middle;
middle = (left + right) / 2;
}
Both versions of code developed for this lab are available in program binary-searches.c. Also, it is useful to observe that both binary search algorithms ran correctly the first time they were run.
We can follow a similar approach to develop code for the binary search, based on the other two loop invariants as well.
Such code development can be the basis for wonderful test questions.
The first part of this reading is based on an on-going project of introducing the concepts of assertions and loop invariants informally in CS1 and CS2 courses. Early funding for this work came, in part, from NSF Grant CDA 9214874, "Integrating Object-Oriented Programming and Formal Methods into the Computer Science Curriculum". Henry M. Walker worked as Senior Investigator on this portion of that effort.
The first four paragraphs describing the binary search are a slightly edited version of Henry M. Walker, Computer Science 2: Principles of Software Engineering, Data Types, and Algorithms, Little, Brown, and Company, 1989, Section 10.1, p. 389, with programming examples translated from Pascal to C. This material is used with permission from the copyright holder.
|
introductory discussion created 25 October 2007 revised 18 January 2009 updated for CS 415 December-January 2021 discussion of binary search created 18 January 2009 updated for CS 415 8 August 2022 merged into a single page 9 August 2022 |
|
| For more information, please contact Henry M. Walker at walker@cs.grinnell.edu. |

|
Copyright © 2011-2022
by Henry M. Walker.
|