Reading on the Bisection Method
Suppose we are given a continuous function f, and we want to
approximate a value r where f(r)=0. (Jargon: r
is called a root of the function f.) While finding
r can be a difficult problem in general, suppose that we can
guess two points a and b (perhaps from a graph) where
f(a) and f(b) have opposite signs. If the graph crosses
the x-axis at the midpoint m of the interval between a
and b (i.e., if f(m)=0), then m is the desired
root of the function. Otherwise, the four possible cases are shown
below:
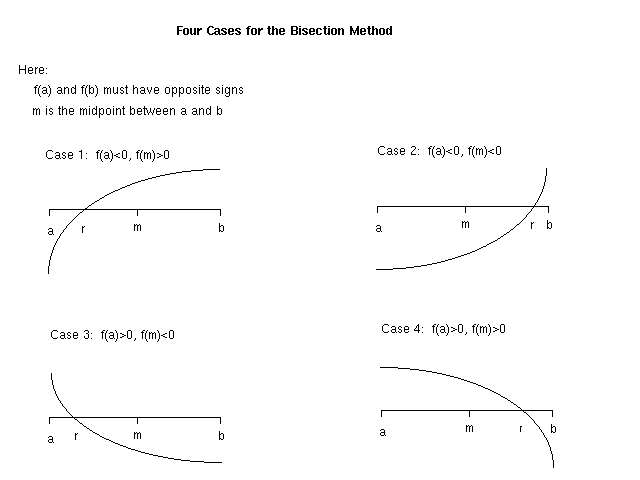
Since this setting assumes we are given a and b for
which f(a) and f(b) have opposite signs, we can
infer that a root r must lie in the interval [a, b]. In
one step, we can cut this interval in half as follows. If f(a)
and f(m) have opposite signs, then r must lie in the
interval [a, m]; otherwise, r must lie in the interval
[m, b].
One simple way to determine if two numbers have the same sign
is to compute their product. If the product is positive, the
two numbers are both positive or both negative. If the product is
negative, one of the original numbers is positive and the other
is negative.
Following this process of cutting the interval in half, we can
continue until the interval is very narrow. At this stage, the
midpoint of the interval will be a reasonable approximation to
a root of the function.
