Consequences of Data Representation on Programming

Data representation has important consequences for designing and writing accurate and reliable programs. Some major issues involve:

• integer overflow

• floating-point overflow, underflow, and round-off errors

• floating-point comparisons in if statements

• floating-point comparisons in loops

• error accumulation

For example, conditional statements may yield unexpected results, loops may not terminate as planned, and computations may accumulate numerical errors.

Integer overflow

The Reading on the Binary Representation of Integers observed that most programming languages, including C, allocate a specified number of bits for the storage of an integer.

• In relatively early computers, 16 bits were allocated to an integer. Thus, signed integers could be in the range -32768 to 32767, and unsigned integers could be in the range 0 through 65535.

• Many modern computers allocate 32 bits for an integer. With this allocation, signed integers can be in the range -2,147,483,648 to 2,147,483,647, and unsigned integers can have the range 0 through 4,294,967,295.

• Some recent computers allocate 64 or more bits, with even larger ranges for signed and unsigned integers.

Whatever the number of bits allocated, integer storage has two essential properties:

• Storage of an integer is exact — approximations to an integer do not arise.

• The size of integers is limited — integers above a maximum bound or below a lower bound cannot be stored.

Processing that attempts to compute and/or store an integer outside the limited range yields a condition called overflow. Hardware sometimes raises error conditions that can be investigated when overflow occurs — but sometimes processing continues with numbers that may have little meaning.

Caution: When applications utilize integer data, programmers must anticipate the potential size of the integers. Integer overflow can have devastating consequences.

Floating-point overflow, underflow, and round-off error

Just as integer values may be too large or too small to be stored in the space allocated for an int, real numbers may be outside the range that can be stored by a float or double. Recall from the Reading on the Binary Representation of Floating-Point Numbers that real numbers are stored in a scientific notation, including a mantissa and an exponent.

• Floating-point overflow arises when the required exponent for a floating-point number is larger than the space available.

• Floating-point underflow arises when the required exponent for a floating-point number too small to be stored.

For float numbers, exponents of two normally must be between -126 and 127, although some adjustments are allowed for positive numbers smaller than 2^-126. When the scientific notation yields 2¹²⁸ or larger, then the number cannot be stored in a float and floating-point overflow occurs. A similar statement applies to underflow.

A different type of issue arises for floating-point numbers, because only 23 bits (single precision) or 52 bit (double precision) are available to store a mantissa. Whenever a mantissa requires additional storage, the number cannot be stored exactly, and an error, called roundoff error, arises.

Perhaps surprisingly, inherent round-off error has a direct impact on the properties of addition, as illustrated by a short computation.

Rather than computing with binary numbers and storing 23 or 52 bits of accuracy, consider the analogous problem of storing decimal numbers with 4 digits of accuracy. When considering 1.000 + 0.0007, the result should be 1.0007. However, only 4 digits of accuracy can be stored, so a choice is needed.

• 1.0007 might be truncated to 1.000
• 1.0007 might be rounded to 1.001

Although either approach is possible, the addition algorithm should be consistent.

Now consider the sum 1.000 + 0.0007 + 0.0007. The specific computation depends upon where parentheses are inserted. Additional may arise, depending upon whether truncation or rounding is used to maintain 4-digits of storage.

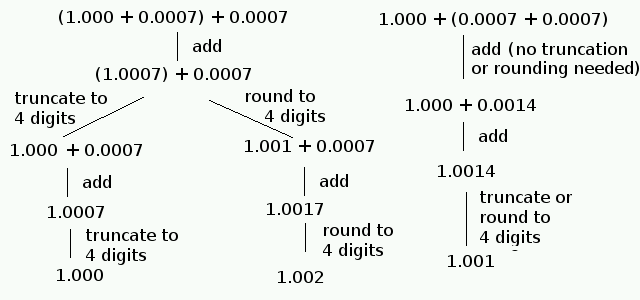
In summary:

• Left associativity with truncating for (1.000 + 0.0007) + 0.0007 produces 1.000 as the arithmetic result.

• Left associativity with rounding for (1.000 + 0.0007) + 0.0007 produces 1.002 as the arithmetic result.

• Right associativity with truncating or rounding for 1.000 + (0.0007 + 0.0007) produces 1.001 as the arithmetic result.

Conclusion: Regardless of whether truncation or rounding is used, left associativity produces a different result than right associativity. That is, addition within the computer is not associative, so many familiar properties of numbers no longer hold!

Floating-point comparisons in if statements

Since real numbers are stored with the potential for round-off error, the actual number stored may be slightly smaller or slightly larger than the intended number. Thus, comparisons with real numbers should take small errors into account.

Example 5 illustrates some difficulties that can arise.

• In Example 5, the decimal number 0.1 (one tenth) is added ten times, with the intention of achieving the number 1.0. However, when double the value stored for one tenth is slightly smaller than the intended value, due to round off. Adding this number several times yields 0.9999999999999999, a number very close to 1.00, but not the same. As a result, a test for equality between the sum and 1.0 fails.

• When Example 5 is changed, so that all numbers are of type float rather than type double the printed sum is 1.0000001192092896 — a number slightly larger than 1.0. In this case, the value stored for one tenth is slighter larger than the intended value.

When testing real numbers, these examples illustrate that some adjustment may be needed to allow for round-off error. For example, a test

  if (result == one)

might be adjusted as follows:

  double allowed_error = 0.01;
  if ((result > one - allowed_error) && (result < one + allowed_error))

Floating-point comparisons in loops

The same issues of round-off errors arise in loops as in comparisons. For loops, such errors may impact the number of times the body of a loop is executed. Example 6 illustrates one type of difficulty.

• Example 6 contains a loop in which the control variable val starts at 0.0 and is supposed to be incremented by one tenth until the value 1.0 is achieved. However, since the loop condition tests for equality of real numbers, the two numbers are never exactly the same, and the loop continues for a very long time.

A somewhat more subtle difficulty arises if the loop in Example 6 is changed, with the intention that the values to be added are 0.0, 0.1, 0.2, ..., 0.9, 1.0. One candidate for the loop condition might be

   while (val <= end)

However, a careful reading of the output from Example 6 shows that the computer would produce the following output within the loop.

val =      0.000000000000000;  sum =      0.000000000000000
val =      0.100000001490116;  sum =      0.100000001490116
val =      0.200000002980232;  sum =      0.300000011920929
val =      0.300000011920929;  sum =      0.600000023841858
val =      0.400000005960464;  sum =      1.000000000000000
val =      0.500000000000000;  sum =      1.500000000000000
val =      0.600000023841858;  sum =      2.099999904632568
val =      0.700000047683716;  sum =      2.799999952316284
val =      0.800000071525574;  sum =      3.599999904632568
val =      0.900000095367432;  sum =      4.500000000000000

Although the intention was for the computer to execute the loop with val having the value 1.0, the next value of val would be 1.000000119209290, a value larger than 1.0, and the loop terminates one iteration early.

As illustrated above, one way to address this problem involves including an allowed-error term:

  double allowed_error = 0.01;
  while (val <= end + allowed_error)

However, this approach would be adding 0.1 to val several times, and we know the value 0.1 is not stored exactly. Thus, each iteration of the loop would be including additional round-off error to our results. To avoid this problem, one might use an integer variable to control the loop.

  int i;
  for (i = 0; i <= 10; i++)
     {
        val = i / 10.0;
        ...

In this approach, the int variable is stored exactly, and the loop guarantees that the loop will be executed the proper number of times. Further, the value of val is recomputed from exact numbers with each iteration. Storage of the resulting real number in val may involve round-off error. However, the round-off error in val will not accumulate from iteration to iteration, since the computation for val begins fresh each time.

Error accumulation

Since the number of bits available to store real numbers is limited, the storage of any floating-point number is subject to some round-off error. Although the amount of error for an individual number may be quite small, these numbers may be used in loops that continue for thousands, millions, billions or more iterations. As a result, round off errors can accumulate.

• In the Vancouver Stock Exchange Index example (Example 4), each computation was stored to three decimal places, with an error of no more than 1 in the third decimal place (an error no more than 0.001). However, such computations were made about 3000 times per day for 22 months. At the end of that time, the computed value was 524.811, and it turned out that the accumulated error was 574.081 — the error was larger than the computed value!

• In Example 6, 0.1 was added repeated to a val variable. Initially, the print out showed round-off error in the 9th decimal place. However, with each iteration, the amount of error increased. By the seventh iteration (with val being 0.600000023841858), a small round-off error appeared in the 8th decimal place. By the 20th iteration (with val being 1.900000333786011), the error in the 8th decimal place was noticeably larger.

Although such accumulated error may have little significance for some applications and computations, the level of inaccuracy may matter significantly in other circumstances. Although a full analysis of accuracy is well beyond the scope of this course, three notes seem appropriate.

1. Whenever floating-point numbers are involved in computations, questions should be asked regarding accuracy. How accurate are the results, and how do you know?

2. The initial discussion of round-off error (near Example 4) considered the sum 1.000 + 0.0007 + 0.0007.

   • In this example, using the large number (1.000) first had the effect of overwhelming the small numbers (0.0007). More generally, adding very small floating-point numbers to large ones may not be noticeable — the addition may be lost in bits that cannot be stored.
   • Adding small numbers first may allow the sums to accumulate (e.g., 0.0007 + 0.0007 = 0.0014), and the result may be large enough to impact the addition of large numbers.

   Overall, a program should add small numbers together before adding the sum to larger numbers; adding numbers in ascending order can be a helpful strategy.

3. The mathematical subject, called numerical analysis, explores the accumulation of numerical error in substantial depth. When an application requires considerable accuracy, investigation of techniques from numerical analysis may be particularly important.