Assignment on Heaps, Sorting and Using Algebra to Improve Efficiency

This assignment is in three parts: Heaps, Heap Sort and Horner's Rule.

Heaps

This section is divided into

• Discussion,
• 0-based indexing of nodes,
• Insertion into a heap, and
• Deletion from a heap.

Discussion

A max-heap is a binary tree with the property that the value at each node is larger (according to some ordering) than the values stored in either child. Similarly, a min-heap is a binary tree with the property that the value at each node is smaller (according to some ordering) than the values stored in either child.

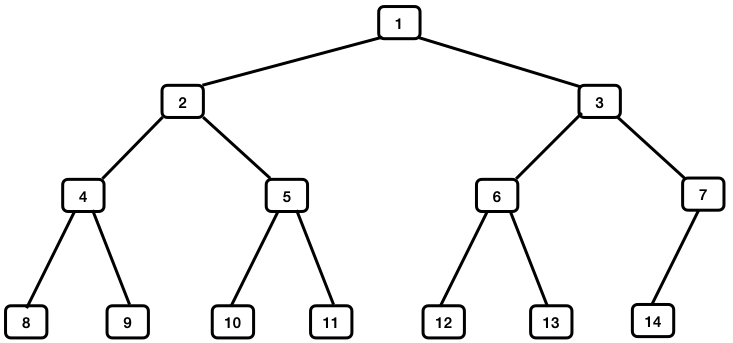
Further, we restrict our attention to trees which are completely balanced. All nodes have 2 children, except at the bottom of the tree. The last row of the tree may not be full, but any items on the last level are moved left as much as possible. For example, the following tree illustrates the shape of a tree and the ordering of values within the tree for a min-heap.

A Simple Labeling of Nodes: Connecting a Heap with an Array

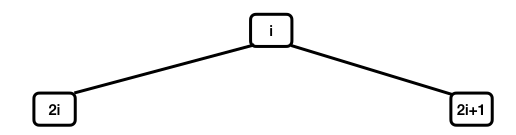
Since nodes in a heap fit a straight forward identification system, there is a natural mapping between the logical nodes in a heap and the indexed elements of an array. To identify the nodes in a tree, the simplest approach is to number the nodes level-by-level from the root downward. Within a level, nodes are numbered left to right. Also, for simplicity, many textbooks assign the index 1 to the root node.

In examining the label nodes, a pattern emerges: for each node labeled i, the left child has label 2*i and the right node has label 2*i+1.

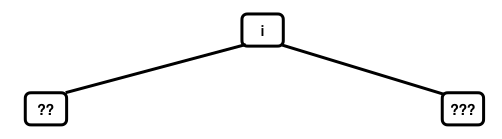
Note: As previously mentioned, some textbooks, such as Data Structures and Problem Solving Using Java, Fourth Edition by Mark Allen Weiss, use this numbering scheme in writing code, with the top node numbered 1. If one considers an array element 0, Weiss suggests filling that position with -∞ for a min-heap or ∞ for a max-heap.

0-based Labeling of Nodes

1. In the context of 0-based labeling, identify a pattern for moving from a node with label j to its left child and its right child. What labels would be found on the left and right nodes of a node with label j?

Insertion into a Heap

In class we considered how to insert an item into a heap and maintain the structure. In each case, we first place the item at the end of a tree (as far left as possible in the last row). The item then is worked up from its position, until the data in the tree are appropriately ordered.

2. The following min-heap repeats the structure given at the beginning of this lab:

   

   Using this min-heap as a start and following the standard procedure to add an element to a heap, insert the values 10, 14, 6, and 12. Show the structure of the tree and the values in each node after each insertion.

Deletion from a Heap

In class, we also considered how to remove the top-priority item from a heap: remove the root as the item to be returned, move the last item from the end of the heap to the root, and work that item down in the heap until the data are properly ordered.

3. Starting with the original heap from the previous problem, use the standard procedure for deleting items from a heap to remove four items in sequence. Show the structure of the tree and the values in each node after each deletion.

Heap Sort

The Heap Sort draws upon the heap data structure, which is discussed in Section 6.4 of the textbook.

1. The key procedure percDown for the Heap Sort has the following specification

   /** *******************************************************************************
    * percDown function                                                              *
    * @param  array  the array to be made into a heap, starting at hold              *
    * @param  hole:  the node index (or base) of subtree for start of processing     *
    * @param  size  the size of the array                                            *
    * @pre   all nodes in left and right subtrees of the hole node are heaps         *
    * @post  all nodes in the tree from the hole node downward form a heap           *
    *********************************************************************************/
   void percDown(int array [ ], int hole, int size)
   

   Implement this procedure, paying attention to the following notes.

   • When processing array elements, assume the heap structure uses 0-based indexing, as discussed above.
   • When working array elements downward within the heap,
     • be sure to check that array access does not go beyond the size of the array.
     • each stage of processing should check only elements in a parent and its children; beyond this checking, processing should not review elements in an entire subtree.

2. Using the percDown procedure, implement a heapSort procedure, with the following specification. (Details may be found in Levitin's text, Section 6.4.)

    /** ******************************************************************************
    * heap sort, main function                                                       *
    * @param  a  the array to be sorted                                              *
    * @param  n  the size of the array                                               *
    * @post  the first n elements of a are sorted in non-descending order            *
    *********************************************************************************/
   

3. Include the heapSort procedure within a complete program that

   • runs the Heap Sort algorithm on arrays of several sizes, including arrays with elements in ascending, random, and descending order.
   • calls procedures to check that whether Heap Sort procedure(s) work properly (and reports the results of the checking).

For the Heap Sort part of the assignment, turn in both a listing of the complete program (including all of Step 4) and the output produced by running the code on several arrays.

Horner's Rule

5. A polynomial function has the form

   p(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₂x² + a₁x + a₀

   Write a function compute_poly that takes three parameters:

   • an x value,
   • an integer n which gives the largest power of x with a non-zero coefficient, and
   • an array a of n+1 coefficients (a₀, a₁, ..., a_n-1, a_n).

   and returns the value of the polynomial p(x).

   Notes:

   • compute_poly should make only one pass through the list of coefficients.
   • Both the number x and the elements of the array a should be real numbers (e.g., of type double) rather than integers.
   • The number x may be used in a multiplication operation no more than n times in the entire computation. (Thus, recomputing xⁱ from scratch for each of the n terms is not acceptable for this problem.)
   • Since the pow function in the math.h library requires many multiplication operations, use of pow in this problem would violate the condition that no more than n multiplications are allowed in the entire solution to this problem. (To be specific, use of pow in this program will yield an automatic score of 0 for this program.)
   • As a hint, you may want to search for discussion of Horner's Rule either in a book on numerical analysis or on the Web.
   • Be sure that the array element a[n] is used as the coefficient of xⁿ (not the coefficient of x⁰).
     For example, if the array is initialized,

       int a = {2, 0, 0, 5};
     

     then the polynomial being evaluated is 5x³ + 2
     Note that a common error in past semesters has been to interpret this initialized array incorrectly, as 2x³ + 5.
   • You will need to include compute_poly in a main program for testing.
   • Be sure your testing covers an appropriate range of cases.
   • compute_poly should return the result of the computation, not print the result. (Any printf statement in compute_poly is subject to a 12 point penalty!)

For this part of the assignment, turn in both a listing of the complete program and the output produced by running the code for several different arrays with varying sizes, including the example given above. Further, for each of your tests, write a short paragraph or present a table that indicates the polynomial being tested (e.g., 2x³ + 5) and indicates the correct value (e.g., result=137) when a specified value (e.g., x=3) is used in the polynomial evaluation. Effectively, this commentary demonstrates that you have looked at the output and can certify that the program works properly. (An answer without this testing/paragraph will be subject to a 10-point penalty. Also, claiming a test is correct when an output value matches an incorrectly computed "correct" value is subject to a 5 point penalty per test case.)

created December 1, 2018 revised December 2, 2018 revised December 27-30, 2021 revised February 4, 2022 reformatted and heap material added July 28, 2022 reorganized with brute force/merge sort added October 3-6, 2022 revised December 30, 2022 reorganized and revised Summer, 2023 reorganized and revised November 30, 2024
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.

Copyright © 2011-2025 by Henry M. Walker. Selected materials copyright by Marge Coahran, Samuel A. Rebelsky, John David Stone, and Henry Walker and used by permission. This page and other materials developed for this course are under development. This and all laboratory exercises for this course are licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 International License.