Assignment on Graph Basics and Singly-nested Loop Invariants
Work for this assignment falls into two groups:
Graph Basics
Adjacency Matrices and Lists
-
Consider the following adjacency matrix S for a weighted
graph. (Note: 0 means there is no edge.)
| | A | B | C
| D | E | F | G
| H | I
|
| A | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 0 | 0
|
| B | 3 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0
|
| C | 0 | 5 | 0 | 0 | 0 | 10 | 0 | 0 | 0
|
| D | 2 | 0 | 0 | 0 | 8 | 0 | 4 | 0 | 0
|
| E | 0 | 0 | 0 | 8 | 0 | 2 | 0 | 5 | 0
|
| F | 0 | 0 | 10 | 0 | 2 | 0 | 0 | 8 | 4
|
| G | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 7 | 0
|
| H | 0 | 0 | 0 | 0 | 5 | 8 | 7 | 0 | 1
|
| I | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 1 | 0
|
-
Draw a picture of the graph represented by this adjacency matrix S, including
the weights.
-
Can this graph be interpreted as being directed? Explain.
-
Can this graph be interpreted as being undirected? Explain.
-
List the vertices in depth-first order beginning with vertex A.
When you have a choice among vertices, pick them in alphabetical
order. (For example, if at some point during the execution of the
algorithm, both vertices B and D needed to be enqueued or pushed
onto a queue or stack, respectively, then B would be
enqueued/pushed before D.)
-
List the vertices in breadth-first order beginning with vertex A.
As in Part 1d, when you have a choice among vertices, pick them in
alphabetical order.
Notes:
- Although several variants of depth- and breadth-first searches
are widely discussed, for this problem, use the algorithms given
in Levitin's textbook.
- If the algorithm allows choice when vertices are placed on a
stack or queue, be sure the vertices are added to that structure
in alphabetical order. (Once in the structure, removal of the
vertices is completely specified by the structure—removal
does not allow choice.)
A Graph Specified by Sets
-
Consider the following graph, specified in terms of sets of
vertices and directed edges.
- G = {V,E}
- V = {A, B, C, D, E, F, G, H, I}
- E = { <A, E, 1 >,
<B, A, 1 >,
<B, C, 2 >,
<B, E, 6 >,
<C, G, 3 >,
<D, H, 3 >,
<E, B, 4 >,
<E, D, 6 >,
<E, I, 4 >,
<F, E, 1 >,
<G, F, 6 >,
<H, I, 3 >,
<I, C, 1 >,
}
-
Write the adjacency matrix for this graph, based upon the
alphabetical ordering of the vertices given.
-
Draw the adjacency list representation for this graph.
-
Can this graph be interpreted as being directed? Explain.
-
Can this graph be interpreted as being undirected? Explain.
-
List the vertices in depth-first order beginning with
vertex E. As in Problem 1, when you have a choice among
vertices, pick them in alphabetical order.
-
List the vertices in breadth-first order beginning with vertex
A. As in Problem 1, when you have a choice among vertices,
pick them in alphabetical order.
Notes:
- Although several variants of depth- and breadth-first searches
are widely discussed, for this problem, use the algorithms given
in Levitin's textbook.
- If the algorithm allows choice when vertices are placed on a
stack or queue, be sure the vertices are added to that structure
in alphabetical order. (Once in the structure, removal of the
vertices is completely specified by the structure—removal
does not allow choice.)
Analytical/Structural Results
-
Suppose a connected graph has v vertices and e edges. What is the complexity of
a breadth-first search?
-
Assume the queue is implemented with an array, and the graph by an
adjacency matrix. Justify your answer.
-
Assume the queue is implemented with a linked list, and the graph
with adjacency lists. Justify your answer.
Invariants for Singly-nested Loops
In this section, you are asked to write two programs, all
involving loop invariants for singly-nested loops. Of course, all
programs must follow the C/C++ Style Guide!
Binary Search Algorithms
-
The Reading
on an Introduction to Loop Invariants discusses two implementations
of a binary search, based on different loop invariants, and
program binary-searches.c
provides the full code for each of these invariants, as well as a
framework for testing these functions.
The reading identifies two variations for the desired result of
a binary search:
-
Return true or false according to whether or not the
item is present.
-
Return the array index where value is found, or return the index of the
first array value larger than the item. (If item is
larger than all items in the array, return the array size — the
index after the last array element.)
Following the second variation as the desired result,
expand binary-searches.c to include a new
function search3 that implements and tests a binary
search that uses the following loop invariant.
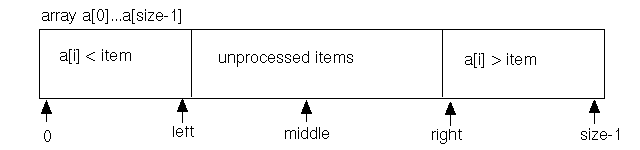
To clarify both the processing and the desired results,
left is the largest array index for which it is
known that a[left] < item (provided some
elements are known to be less than item, or equivalently
left is the first index for
which a[left+1] is unprocessed (provided some
elements have not yet been examined).
right is the smallest array index for
which a[right] > item (provided some elements
are known to be larger than item), or equivalently
right is the first index for which it is known
that a[right-1] is unprocessed (provided some
elements are known to be larger than item)
- the valued returned by the function should be as follows:
- if the desired value is found in the array, the index
of the element should be returned. (If the desired value
appears several times in the array, then the index of any
of those repeated values may be returned.)
- if the desired value is not found, then the search
should return the following:
- if the desired value is smaller than at least
one array element, then the index of the first element in the
array larger than the desired value should be returned.
- if the desired value is larger than all elements
in the array, then the size of the array should be
returned.
To clarify the required return value, consider the following
array of 13 elements:
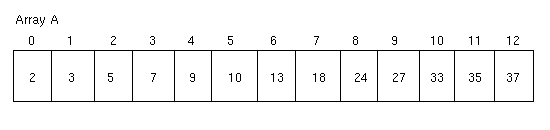
-
If the array is searched for the number 7, then index 3 is
returned.
-
If the array is searched for the number 8, then the index 4 is
returned (the value 9 in the array is the first value bigger
than 8, so its index is returned.
-
If the array is searched for the number 39, then the size of the
array (13) is returned, as all elements in the array are
smaller than 39.
The Second Smallest Element in an Array
Consider the following problem. Given an array a with n distinct integer
numbers, find the second largest number of the array. (Note that no
assumptions are made regarding the nature of the integers—they
could be small or large, negative, positive, zero, or a combination.)
This problem can be solved in many ways. For example,
-
Sort array and return the second element from the end.
-
Scan the entire array to locate the largest element, swap
that the largest element with the last element in the array, scan
all the the last element in the array and return the result of the
second scan.
-
Keep track of the largest and second largest elements in a single
scan of the array.
This problem follows the third approach, utilizing a specified loop
invariant.
-
Write a program to find the second largest element in an array a
of size n, utilizing a single pass through the array.
After reading the array size n and the array elements, the
program should have a single loop that starts at some value ??
and proceeds through the array:
for (i = ??; i < n; i++)
with the following loop invariant: for each i
- variable
largest holds the value of the largest
element in a[0..i-1]
- variable
second holds the value of the
second largest elementin a[0..i-1]
At the end of processing, the program should print the second
largest elementin the array.
Notes:
-
In your code, you will need to decide where the loop should
start and write a loop body that maintains this loop invariant
for all i.
-
Once your code is finalized and tested with several array
values, you should provide an argument why the program is
correct, based on this invariant:
- Why is this invariant before the loop first begins?
- Assuming the invariant is true before a loop iteration,
why must the invariant be true after the iteration
- Why does this invariant insure the program identifies the
correct result when the loop is completed?
created August 7, 2022
revised August 9, 2022
revised December 29, 2022-January 2, 2023
minor editing February 15 and 22, 2023
revised December 5, 2024
|


|
|
For more information, please contact
Henry M. Walker at
walker@cs.grinnell.edu.
|


