Abstract
Many applications require that data be ordered and maintained.
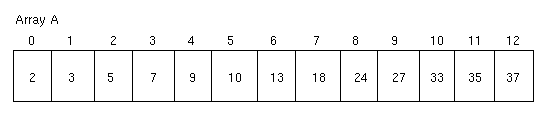
In C and many other languages, a simple way to structure ordered data
is in an array (or vector), such as the following ordered array
A of integers.
| CS 415, Section 001 | Sonoma State University | Spring, 2024 |
|
Algorithm Analysis
|
||
|
Instructor: Henry M. Walker
Lecturer, Sonoma State University | ||
Although much of this course has been well developed in recent semesters, the SSU CS faculty recently have approved a partially-updated course description. Currenly, the Web site is reasonably stable, but modest refinements are possbile.
Since May, 2024, the California Faculty Association (CFA) – the labor union of professors, lecturers, librarians, counselors, and coaches across the 23 California State University campuses – has been in negotiations with the management of the California State University System. After a one-day strike on Monday, January 22, the two sides have reached a tentative agreement, and the strike has been called off. Effective Tuesday, January 23, SSU classes (including CS 415) will be held as scheduled.
Many applications require that data be ordered and maintained.
In C and many other languages, a simple way to structure ordered data
is in an array (or vector), such as the following ordered array
A of integers.

One common sorting approach is based on code that assumes that the first part of an array is ordered and then adds successive items to this array segment until the entire array is sorted.
Some examples of humans manually using insertion sort include sorting a deck of cards, or sorting books on a bookshelf.
To understand this approach within an array, we first consider how to add one item to an ordered array segment. We then apply this work to each array element in turn to yield an ordered array.
Suppose items A[0], ..., A[k-1] are ordered in array A:
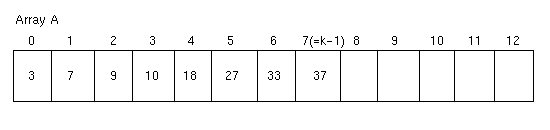
To insert an item into the first part of this array and maintain the ordering, we proceed from right to left with elements in the array.
We compare item to successive elements at the right of the array.
Once we move elements larger than item to the right, there is room to insert item in its place.
For example, the following figure shows the insertion of the number 15 into the array A above.
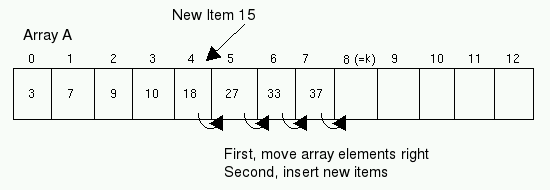
The following code translates this idea into C. When this code terminates, item is placed into the array, so that items A[0], ..., A[k] become ordered:
int i = k-1;
while ((i >= 0) && a[i] > item){
a[i+1] = a[i];
i--;
}
a[i+1] = item;
Using this basic insertion step, an array A can be sorted iteratively according to the following outline:
Animation borrowed
from Wikipedia.org
under a Creative Commons license.
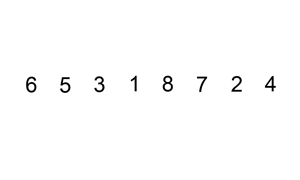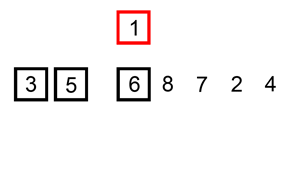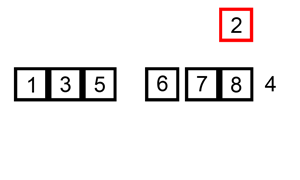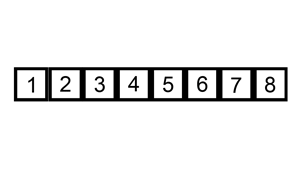
This outline gives rise the the following code, called an insertion sort.
void insertionSort (int a [], int length) {
// method to sort using the insertion sort
// parameters: a, the array to be sorted
// length, the size of the a array
for (int k = 1; k < length; k++) {
int item = a[k];
int i = k-1;
while ((i >= 0) && a[i] > item){
a[i+1] = a[i];
i--;
}
a[i+1] = item;
}
}
It is important to notice that the item being compared is not swapped with each item as the loop progresses. The items that are compared against are shifted; after the comparisons, the element being compared is inserted after any large items.
The array parameter for insertionSort may be specified in either of two, interchangeable ways:
int a [] (used here) emphasizes that parameter a will be an array of int values.
int * a highlights that an array parameter is the base address of an array of int values. From this perspective, the base address of an array is the address of the initial int value or an int .
As already noted, the two parameter declarations are equivalent and may be used interchangeably.
This sorting algorithm has several helpful properties.
The insertion sort is
relatively simple,
efficient for small data sets and data sets that are already partially sorted,
stable in the sense that it does not switch identical elements, and
only requires a constant amount of additional memory space (that is, the amount of memory for the set of elements, plus memory for one element of the set).
The amount of time this algorithm takes to sort a set is dependent upon the set itself.
For any data set, each successive array element must be compared to the array element just before it.
In the best case, each successive array element will already be larger than its predecessor, and no array elements will need to be moved.
In the worse case, each successive array element will be smaller than its predecessors, and all array elements on the left will need to be moved to the right with each insertion.
If the array data start in random order, each successive array element will be larger than some elements to its left and smaller than other. On average, we might have to shift about half elements on the left over to make room for successive array elements.
Overall, for a set with n elements, if the set is sorted (or nearly so), the algorithm takes only a single time unit for each element, so it takes n time units. On the other hand, if the set is in reverse order (that is, largest to smallest), the time approaches n-squared. You will see the previous two statements proven in a later course.
|
created 1 August 2011 by April O'Neill revised 5 August 2011 by April O'Neill minor editing 7 November 2011 by Henry M. Walker altered sort header 5 December 2012 by Henry M. Walker updated and reformatted August-November 2016 by Henry M. Walker revised January 2023 by Henry M. Walker revised Summer 2023 by Henry M. Walker |
|
| For more information, please contact Henry M. Walker at walker@cs.grinnell.edu. |