Assignment on Consequences of Data Representation

This assignment explores some practical consequences of the representation of data in program processing.

Integer Overflow

Recall from your prior work in C/C++ that constants variables INT_MIN and INT_MAX in C/C++ contain the smallest and largest int values available in C/C++.

1. Finding Integer Averages: Given two integers, i and j, a program is supposed to compute their average (as an integer).

   Notes:

   • In case the arithmetic average is a real number ending in .5, the average may be rounded either up or down. Thus, either 7 or 8 should be considered as a correct [integer] average of 6 and 9.
   • In the case that the integers, i and j, are the same, their average (of course) should be i (or j). Thus, the average of 5 and 5 should be 5, and the average of 6 and 6 should be 6.
   • A program should avoid issues of overflow to the extent possible. (Pragmatically, arithmetic with INT_MIN and INT_MAX may be troublesome, but such difficult cases should be kept to a minimum.)

   Five approaches are proposed to find this average:

         avg1 = (i + j) / 2;
         avg2 = i/2 + j/2;
         avg3 = (i+1)/2 + j/2;
         avg4 = (i+1)/2 + (j+1)/2;
         avg5 = i + (i-j)/2; 
       

   1. Which, if any, of these approaches will work reliably for all (or almost all) non-negative integers i and j? Explain.
   2. Suppose i and j may be any integers—positive, negative, or zero. In this general case, which, if any, of these approaches will work reliably for all (or almost all) values of i and j? Explain.

2. Consider the program integer-average.c.

   1. Compile and run the program, and record what int values are possible within C proprams.
   2. Review the program to determine how the values of arr1 are computed, and how the value of sum compares to INT_MAX
   3. Check the program output. Is the computation of the average of values for arr1 correct?
   4. Answer parts b and c for array arr2. What is different in the processing? To the extent that you can, explain why the average computation for this array yields an incorrect result.

Storage of Real Numbers and its Accuracy

The international standard for 64-bit floating-point numbers (often the basis for a double in C/C++) uses a binary version of scientific notation, with a sign, an exponent (a power of 2 in binary) and a mantissa (also as a binary number). With the internation standard for 64-bit floating point numbers, the bits are allocated as follows:

• 1 bit: sign (plus or minus)
• 11 bits: an exponent
• 52 bits: the mantissa

See Binary Representation of Floating-point Numbers for details.

In practice, this international binary standard does not store the leading mantissa bit (because in scientific notation for binary numbers, the leading bit is always 1 (the number 0 is treated in a different way). Thus, the 64-bit standard effectively stores 52 bits for the mantissa, so this format can provide 53 bits of accuracy for stored numbers.

In binary, the decimal number 1023 can be represented with 10 bits; that is the decimal number 1,000 can be stored in about 10 binary bits, and 3 decimal-digit numbers require 10 binary bits. Using this perspective, the decimal number 1,000,000 can be stored with about 20 bits, and about 6 decimal-digit numbers require about 20 bits. Continuing this insight, about 15 decimal-digit numbers require about 50 bits.

Also, the decimal digit 8 requires about 3 binary bits, so 3 binary bits allows storage for roughly another decimal digi).

Putting these observations together, we might expect that the 53-bits utilized in the 64-bit international standard can store about 16 decimal digits of accuracy.

To gain first-hand experience with the storage of double numbers in C/C++, this exercise considers the storage of the number Pi. According to Britannica.com, the value of Pi to 39 decimal places is 3.141592653589793238462643383279502884197.

3. To investigate the storage of double numbers, the program pi-storage.c prints the number Pi to several decimal places of accuracy.

   Download, compile, and run this program.

   1. How does the program store and print the value of Pi exactly to 39 decimal places of accuracy? That is, how are the 39 digits stored and printed exactly?
   2. The output of the program is organized into groups of lines. Describe what is printed on each line of a group. Also, indicate how each output line is obtained. (You may need to consult a C/C++ manual to understand some functions, such as sprint.)
   3. printf tries to round a double to the number of decimal places specified. For the output involving 13 to 16 decimal places, does the output reflect this rounding?
   4. What can you say about rounding (or the lack thereof), when 17 or more decimal places are printed?
   5. As the number of digits are printed (after 17 decimal places), what can you say about the accuracy of the double number printed? Why do you think this accuracy is (or is not) observed?

Associativity of Addition for Real Numbers

Over the years, many approaches have been developed to compute the value of the number π. Many of these approaches are based on an infinite series, one of which is

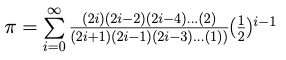
Details behind this formula may be found in a Wikipedia article on Leibniz formula for π and a stockexchange article on Series that converge to π quickly.

Although this is an infinite sum, calculus (and algebra) indicates that successively better approximations to π may be obtained by including more and more terms of the series. Also, it is worth noting that computationally each term is smaller than the previous.

Program pi-approx.c

• asks the user how many terms n in the series to compute,
• computes the desired number of terms,
• computes and prints the sum, starting from term i=0 to i=n-1 (that is, starting with the largest term and adding successive smaller terms), and also
• computes and prints the sum, starting from term i=n-1 to i=0 (that is, starting with the smallest term and adding successive larger terms).

4. Download, compile, and run program pi-approx.c

   1. In reading the program, how are successive terms in the series computed—explain briefly why this approach gives the desired sum of terms.
   2. Describe the output generated with the number of terms being 10, 25, 40, 50, 60, 100, and 1000.
   3. To what extent does including more terms to the sum help the accuracy when computing from the largest term to the smallest? Explain.
   4. To what extent does including more terms to the sum help the accuracy when computing from the smallest term to the largest? Explain.
   5. If there is a difference when computing from largest term to smallest versus smallest term to largest, explain the difference. What, if any, conclusions are suggested by the outputs observed from this exercise?

Compounding of Numeric Error

Our discussions of the representation of real numbers (doubles and floats) have identified at least three factors that can cause errors in processing—particularly if the errors can accumulate as processing continues.

• numerical errors can accumulate in some situations, as processing continues (particularly in loops that are repeated many times,
• loops may not continue through the proper number of iterations,
• the order of addition can make a difference:
  • if small numbers are added to large ones, the small numbers may be lost
  • if small numbers are added together first and then to large ones, then the small values may have an impact in the overall sum

Be sure to take these potential troubles into account in answering Steps 4 and 5.

5. Given that start < end, suppose a loop is to begin at start and finish at (or near) end in exactly n+1 iterations. Within this loop, suppose the control variable will increase by a computed value increment = (end-start)/n with each iteration.

   Two loop structures are proposed:

         // approach 1
         increment = (end - start)/n;
         for (i = 0; i <= n; i++){
              value = start + i * increment;              
             /* processing for value */
           }
       

         // approach 2
         value = start;
         increment = (end - start)/n;
         while (value <= end) {
            /* processing for value */
            value += increment;             
         }
       

   Although the first approach requires somewhat more arithmetic within the loop than the second, it likely will provide better accuracy. Identify two distinct reasons why the first approach should be preferred over the second.

6. Suppose y = f(x) is a function that decreases significantly from x=a to x=b, on the interval [a, b], with a < b.

   Throughout this interval, assume f(x)>0, and assume the Trapezoidal Rule were to be used to approximate the area under y = f(x) on the interval [a, b].

   1. Assuming accuracy is the highest priority for this computation, should the main loop begin at a and go toward b or begin at b and go toward a, or is either order fine? Explain.

   2. Again, assuming accuracy of the answer is the highest priority, write a reasonably efficient code that implements the Trapezoidal Rule for this function on this interval. (To be reasonably efficient, f(x) should be computed only once for each value of x, and division by 2 should be done as little as possible, as discussed in class.)
      Be sure to include your code within a program, and run several tests of the program.
      
      For this step, submit both the program and the output from several test runs.
      
      (Of course, your program must conform to the course's C/C++ Style Guide.)

   3. Explain how and why your approach to this problem (with f(x) decreasing significantly from x=a to x=b) should be different from the code when f(x) increases over this interval.