CS 415, Section 001 Sonoma State University Spring, 2023
 
Algorithm Analysis
Instructor: Henry M. Walker

Lecturer, Sonoma State University
Professor Emeritus of Computer Science and Mathematics, Grinnell College

Although much of this course is well developed, some details can be expected to evolve as the semester progresses.
Any changes in course details will be announced promptly during class.

Assignment on Approximation Methods

Approximation Algorithms for the Traveling Salesperson Problem

  1. Pages 438-440 of the textbook describe how to use a Branch-and-Bound algorithm to find an approximate solution to the Traveling Salesperson Problem, and pages 444-448 describe a "Twice-around-the-tree" algorithm that uses a different approach to approximate a solution.

    1. Graph A
      Graph A
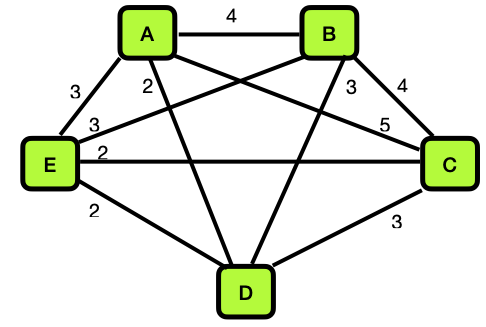
      • For Graph A, consider both the Branch-and-Bound Algorithm and the "Twice-around-the-Tree" Algorithm. In each case,
        • If the algorithm can be applied to the graph, use that algorithm to approximate a solution to the Traveling Salesperson Problem.
        • if the graph does not meet the required assumptions for the algorithm, indicate what condition(s) is(are) violated, rather than applying the algorithm.
    2. Graph B
      Graph B
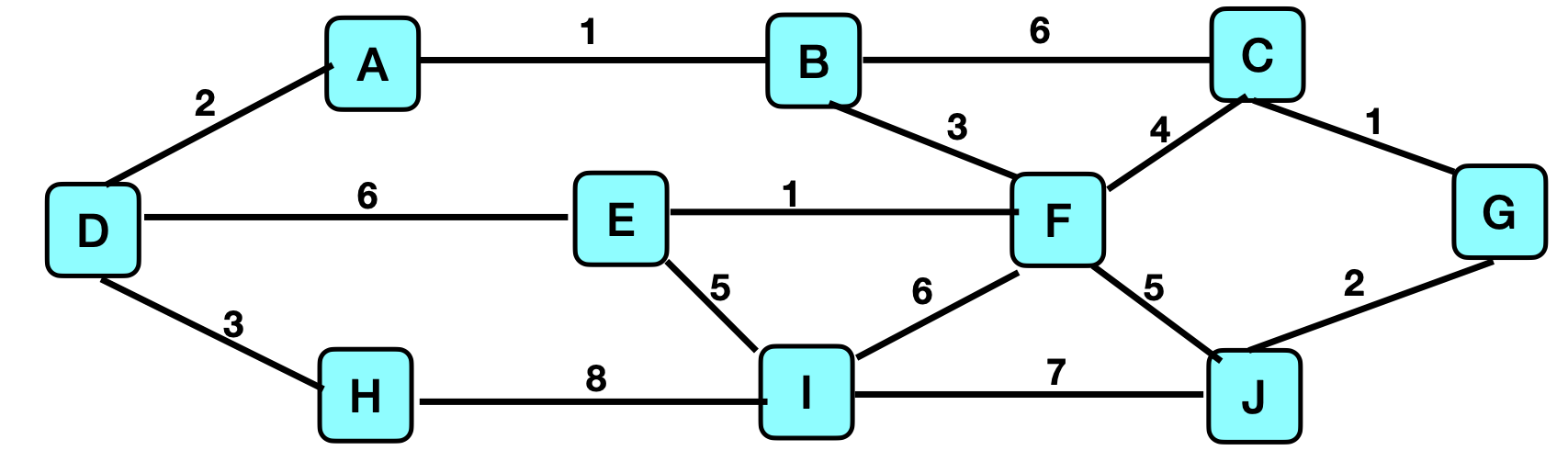
      • For Graph B, consider the "Twice-around-the-Tree" Algorithm. (In the interests of time, DO NOT use the Branch-and-Bound Algorithm for this graph!)
        • If this algorithm can be applied to the graph, use the algorithm to approximate a solution to the Traveling Salesperson Problem.
        • if this graph does not meet the required assumptions for the algorithm, indicate what condition(s) is(are) violated, rather than applying the algorithm.

Approximation Algorithms for Roots of a Function

Suppose we are given a continuous function f, and we want to approximate a value r where f(r)=0. (Jargon: r is called a root of the function f.)

This section considers two approximation methods for finding the roots of functions, the bisection method and Newton's Method.

Work with these numeric methods requires you to graph functions, so that you have a visual representation of a function's graph. For this purpose, you can use any graphing software that you like. One option is Graph a function from desmos.com.

The Bisection Method

The following question is based on the Reading on the Bisection Method.

  1. Write a program that uses the Bisection Method to approximate a root of a function.

    • The start of the program should define a function 
      double f (double x)

      for which the program is to find a root.

    • The program should define a new function 
      double find_root (double a, double b, double accuracy)

      which works as follows:

      • find_root should use an assert statement to check that f(a) and f(b) have different signs. (The program should terminate if this assumption is not met.)
      • Another assert statement at the beginning of find_root should check that the accuracy is positive.
      • find_root should continue to cut the interval in half, following the Bisection Method, until either f(m)=0 for a computed midpoint m or the newly computed interval is shorter than the accuracy specified.
      • find_root should return the computed midpoint of the final interval.
    • The main program should ask the user to enter endpoints a and b and the accuracy. The main program then should call find_roots with the appropriate parameters and report the result.

Newton's Method

Consult Levitin's textbook, Section 11.4 for details on Newton's Method, including the main formula.

  1. Use the program newtons-method.c to apply Newton's method to solve the following.

    1. Solve the equation x3 - 4x2 - 1 = 0.
      • Graph f(x) = x3 - 4x2 - 1 = 0 using Graph a function from desmos.com or other graphing software.
      • The program newtons-method.c is already set up for the function f(x) = x3 - 4x2 - 1 = 0.
      • After you compile and run the program, it will ask you for an initial guess. Use the graph you obtained above to determine a reasonable choice. What solution does the program produce?

    2. Find the cube root of n by solving the equation f(x) = 0 where f(x) = x3 - n. In particular, use the program with this function (and its derivative) to find the cube root of 27.

      • About how many iterations are needed to get a stable result, if you choose 1 as the initial value for x0.
      • Does using 27 as the initial value for x0 require more, fewer, or about the same number of iterations to obtain a stable result? Explain briefly.
      • Check your answer. If you know the cube root of 27 without help, just give the answer and explain how you knew the answer. If you need a calculator, feel free to use one, but again describe briefly what buttons you used. (Many calculators use Newton's Method, with an initial guess of 1, to take square and cube roots.)
      • Repeat parts a, b, and c to find the cube root of 21.
created May 2, 2022
revised May 3, 2022
revised May 7, 2022
revised July 22, 2022
revised December 31, 2022–January 3, 2023
revised Summer 2023
revised April 9, 2024 		Valid HTML 4.01! Valid CSS!
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.