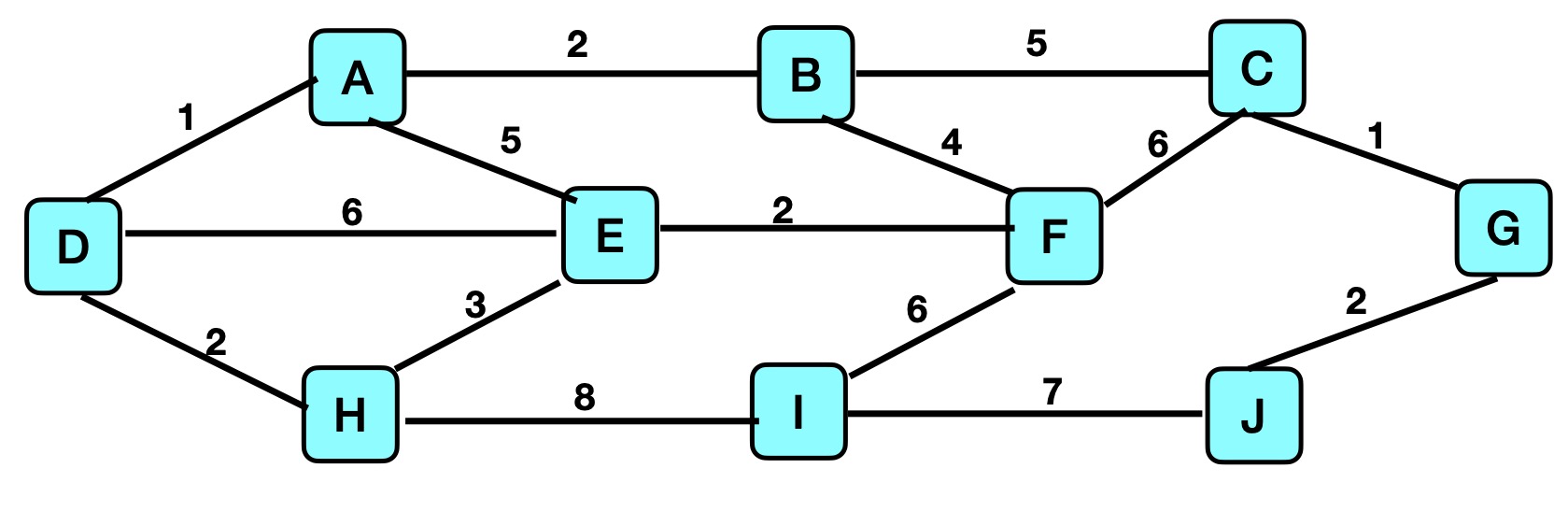
Apply each of these algorithms to find approximate solutions to the Traveling Salesperson Problem for each of the following graphs.
- Graph A
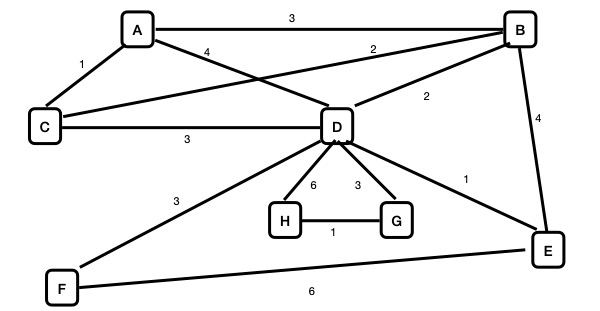
- Graph B
| CS 415, Section 002 | Sonoma State University | Spring, 2022 |
|
Algorithm Analysis
|
||
|
Instructor: Henry M. Walker
Lecturer, Sonoma State University | ||
The Halting Problem is said to be "unsolvable".
A company believes there would be a strong market for a software package that would take the specifications of a problem and the code for a program as input and would prove whether the program meets its specifications in all cases. That is, the software package would prove whether or not a program always meets its specifications. Should the company invest in the development of such a software package? Why or why not? Explain.
Consider the concepts of a NP-Hard problem and an NP-Complete problem.
State two problems that are in Class P, and justify your conclusion for each problem.
Given a Boolean expression with n variables, the Satisfiability Problem asks whether there is an assignment of True or False to each of the variables, so that the resulting expression is True. Give a careful argument, using the formal definition of Class NP, that explains why the Satisfiability Problem is in Class NP.
In Levitin's textbook, solve Problems 2 and 3 in Section 11.3.
Suppose a loop is to start at a value start and
finish at (or near) a value end in
about n+1 iterations, with
iterations increasing by a
value increment = (end-start)/n each
time.
Two loop structures are proposed:
// approach 1
increment = (end - start)/n;
for (i = 0; i <= n; i++){
value = start + i * increment;
/* processing for value */
}
// approach 2
value = start;
increment = (end - start)/n;
while (value <= end) {
/* processing for value */
value += increment;
}
Does either of these approches have any advantages over the other and thus be preferred, or are the two approaches about the same in computing a reliably-accurate answer? Explain.
In reviewing Approach 2 in the previous problem, what, if any, adjustments would you suggest to improve the code (e.g., to ensure the loop is repeated n+1 times). Briefly explain.
Suppose y = f(x) is a function that decreases
from x=a to x=b, on the interval
[a, b], with a<b.
Throughout this interval, assume f(x)>0, and
assume the Trapezoidal Rule were to be used to approximate the
area under y = f(x) on the interval
[a, b].
start and go
toward end or begin at end and go
toward start, or is either order fine? Explain.
Pages 438-440 of the textbook describe how to use a Branch-and-Bound algorithm to find an approximate solution to the Traveling Salesperson Problem, and pages 444-448 describe a "Twice-around-the-tree" algorithm that uses a different approach to approximate another solution.
Apply each of these algorithms to find approximate solutions to the Traveling Salesperson Problem for each of the following graphs.


Suppose we are given a continuous function f, and we want to approximate a value r where f(r)=0. (Jargon: r is called a root of the function f.)
This section considers two approximation methods for finding the roots of functions, the bisection method and Newton's Method.
Work with these numeric methods requires you to graph functions, so that you have a visual representation of a function's graph. For this purpose, you can use any graphing software that you like. One option is Graph a function from desmos.com.
x^4.
Although finding a root r of a function can be a difficult problem in general, suppose that we can guess two points a and b (perhaps from a graph) where f(a) and f(b) have opposite signs. If the graph crosses the x-axis at the midpoint m of the interval between a and b (i.e., if f(m)=0), then m is the desired root of the function. Otherwise, the four possible cases are shown below:
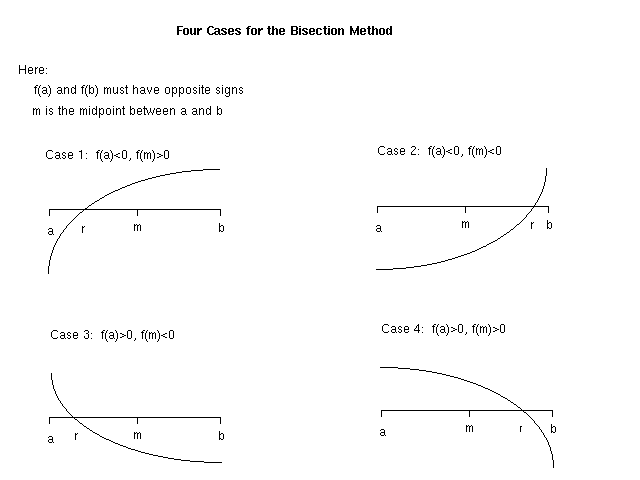
Since this setting assumes we are given a and b for which f(a) and f(b) have opposite signs, we can infer that a root r must lie in the interval [a, b]. In one step, we can cut this interval in half as follows. If f(a) and f(m) have opposite signs, then r must lie in the interval [a, m]; otherwise, r must lie in the interval [m, b].
One simple way to determine if two numbers have the same sign is to compute their product. If the product is positive, the two numbers are both positive or both negative. If the product is negative, one of the original numbers is positive and the other is negative.
Following this process of cutting the interval in half, we can continue until the interval is very narrow. At this stage, the midpoint of the interval will be a reasonable approximation to a root of the function.
Write a program that uses the Bisection Method to approximate a root of a function.
double f (double x)
for which the program is to find a root.
double find_root (double a, double b, double accuracy)
which works as follows:
This section draws heavily upon a lab by a similar name in Learning by Discovery: A Lab Manual for Calculus, edited by Anita Solow, MAA Notes, 1993. In particular, the approach and many details here come from a 1993 lab by Anita Solow.
Given a function f, we want to approximate a solution to f(x) = 0. To use Newton's Method, we must have an initial guess x0. The next guess, x1, is found at the intersection of the x-axis with the tangent line to y = f(x) at (x0, f(x0)), as shown in the following figure:
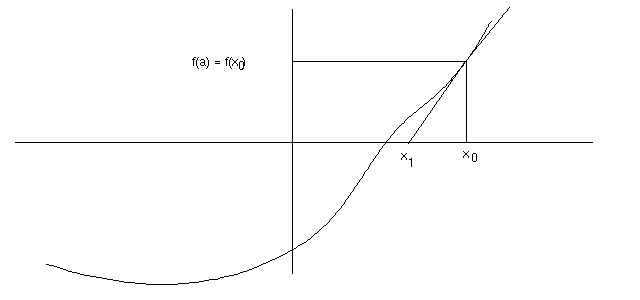
We need to find a formula for x1.
Once we have x1, we repeat the process to get x2 from x1, x3 from x2, etc. If all goes well, the xi ' s get closer and closer to the zero of f that we are seeking.
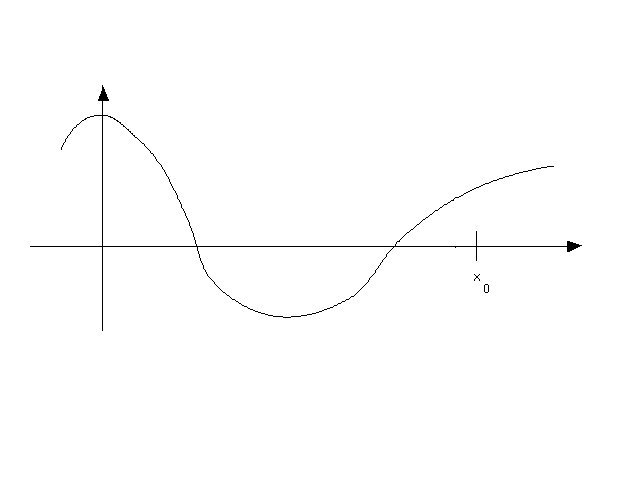
Much of the rest of this worksheet requires use of graphing software to plot graphs and a program newtons-method.c to perform computations.
You can use Newton's Method to find square roots of numbers. For example, to find the square root of n, solve the equation f(x) = 0 where f(x) = x2 - n.
|
created May 2, 2022 revised May 3, 2022 revised May 7, 2022 |
|
| For more information, please contact Henry M. Walker at walker@cs.grinnell.edu. |