Worksheet:  Huffman Trees, Minimum Cost Spanning Trees, Classes P and NP

Huffman Trees and Codes

1. Huffman Algorithm

   1. Construct a Huffman tree from the following set of frequencies. (Always put the smaller subtree to the left. If there is a tie, put the leaf to the left.)

      a	b	c	e	g	i	j	o	m	n	p	r	s	t	u	<space>
      2	1	4	4	1	2	1	1	1	1	1	2	3	3	2	5

   2. Using your tree in Part a, encode the message "computer science is a great subject".
2. Repeat the previous problem with the following table of frequencies

   a	e	i	e	o	u	s	t
   1	3	5	2	4	6	7	8

3. Decode the front of the AP Computer Science t-shirt for 2002.

Minimum Cost Spanning Trees

4. Consider the following undirected graph:

   

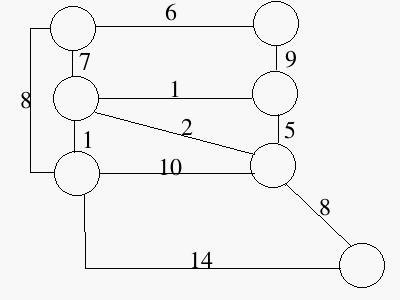
   Find the minimum cost spanning tree, showing the main steps in applying the algorithm.

5. Repeat the previous problem for the following graph.

   

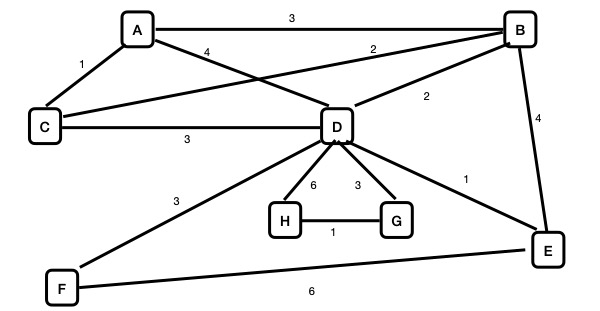
6. Given an undirected graph, a minimum cost spanning trees need not be unique. Given an example of a graph with two different minimum cost spanning trees, where the graph has the fewest number of vertices and the fewest number of edges. In addition to displaying the graph and the two different minimum cost spanning trees, provide an explanation as to why this graph is the smallest possible with two different such trees.

Classes P and NP

7. Consider the terms, "Class P", "Class NP", "NP-Complete", "NP-Hard", tractable, intractable, decidable, and undecidable.

   1. Give careful definitions of each of these terms..
   2. Identify 3 problems in Class P, and explain why each is in Class P.
   3. Use the definition of Class NP to explain why the Hamiltonian Path problem and the Course Scheduling Problem are in Class NP.

8. Answer problem 11 in Levitin's textbook (page 411), and explain your answer in each case.

created April 25, 2022 revised April 25, 2022
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.