Worksheet:  Graph Algorithms

Instructions:

• As with all work for this course, each problem submitted must include a complete list of all sources used (e.g., from the textbook, Web materials, conversations with other students, etc.) References must be specific, indicating publication information (e.g., publisher, date, Web site URL) or individual(s) consulted.
• Grading will be based on the insight and comprehension shown in the student work. Thus, copying an answer from another source may yield few or no points.

Elementary Graphs

Consider the following as the adjacency matrix S for a weighted, directed graph. (Note: 0 means there is no edge.)

1. Draw a picture of the graph represented by this adjacency matrix S without the weights.

2. Is this graph directed or undirected? Explain.

3. List the vertices in depth-first order beginning with vertex A. When you have a choice among vertices, pick them in alphabetical order.

Graph of Course Prerequisites

4. Refer to the Diagram of the SSU Computer Science curriculum for the current SSU/CS curriculum. Arrows in the diagram represent prerequisites, and dotted lines of co-requisites should be ignored.

   1. Apply the topological sort algorithm to this digraph, or explain why it cannot be applied.
      • If a topological sort algorithm cannot be applied to this graph, explain why.
      • If a topological sort can be applied to this graph,
        • Show the steps involved in applying Prim's algorithm.
        • Show the steps involved in applying Kruskal's algorithm.
   2. List the vertices obtained in a breadth-first search, starting with the CS 115 vertex. When you have a choice of which item to enqueue next, pick the one with the lowest course number.
   3. List the vertices obtained in a depth-first search, starting with the CS 115 vertex. Again, use the course number to decide which vertices to use first.

A Directed Graph

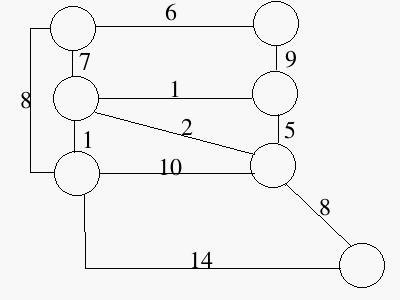
5. Consider the following directed graph:

   
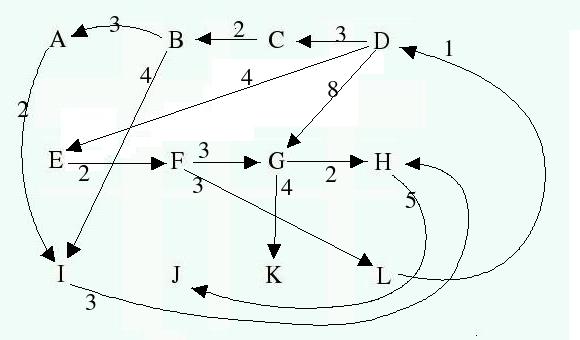
   1. Consider applying the topological sort algorithm to this digraph, and follow the same instructions as given for Problem 4, above.
   2. Show the steps and computations involved in identifying the strongly-connected components of this graph.
   3. Considering this graph as being undirected, find a minimum-cost spanning tree.

Minimum Cost Spanning Trees

7. Consider the following undirected graph:

   

   Find the minimum cost spanning tree, showing the main steps in applying the algorithm.

8. Given an undirected graph, a minimum cost spanning trees need not be unique. Given an example of a graph with two different minimum cost spanning trees, where the graph has the fewest number of vertices and the fewest number of edges. In addition to displaying the graph and the two different minimum cost spanning trees, provide an explanation as to why this graph is the smallest possible with two different such trees.

Huffman Codes

9. Huffman Algorithm

   1. Construct a Huffman tree from the following set of frequencies. (Always put the smaller subtree to the left. If there is a tie, put the leaf to the left.)

      a	b	c	e	g	i	j	o	m	n	p	r	s	t	u	<space>
      2	1	4	4	1	2	1	1	1	1	1	2	3	3	2	5

   2. Using your tree in Part a, encode the message "computer science is a great subject".

10. Decode the front of the AP Computer Science t-shirt for 2002.

Algorithm Choices

11. The Huffman algorithm generates a tree with a guaranteed minimum external path length. The optimal binary search tree algorithm generates a tree with a guaranteed minimum cost, where the cost minimizes the weighted internal and external path lengths.

    If all of the internal node weights of a binary tree are 0, then the internal path length must be 0, so the total cost is the same as the external path length. Does this mean that the Huffman algorithm and the optimal binary search tree algorithm give the same result? Justify your answer.

created October-December, 2014 revised December-January 2021
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.