Worksheet:  More Trees

Instructions:

• Collaboration is allowed on these problems.
• As with all work for this course, each problem submitted must include a complete list of all sources used (e.g., from the textbook, Web materials, conversations with other students, etc.) References must be specific, indicating publication information (e.g., publisher, date, Web site URL) or individual(s) consulted.
• Grading will be based on the insight and comprehension shown in the student work. Thus, copying an answer from another source may yield few or no points.

Problems

1. Consider the following two binary search trees:

   
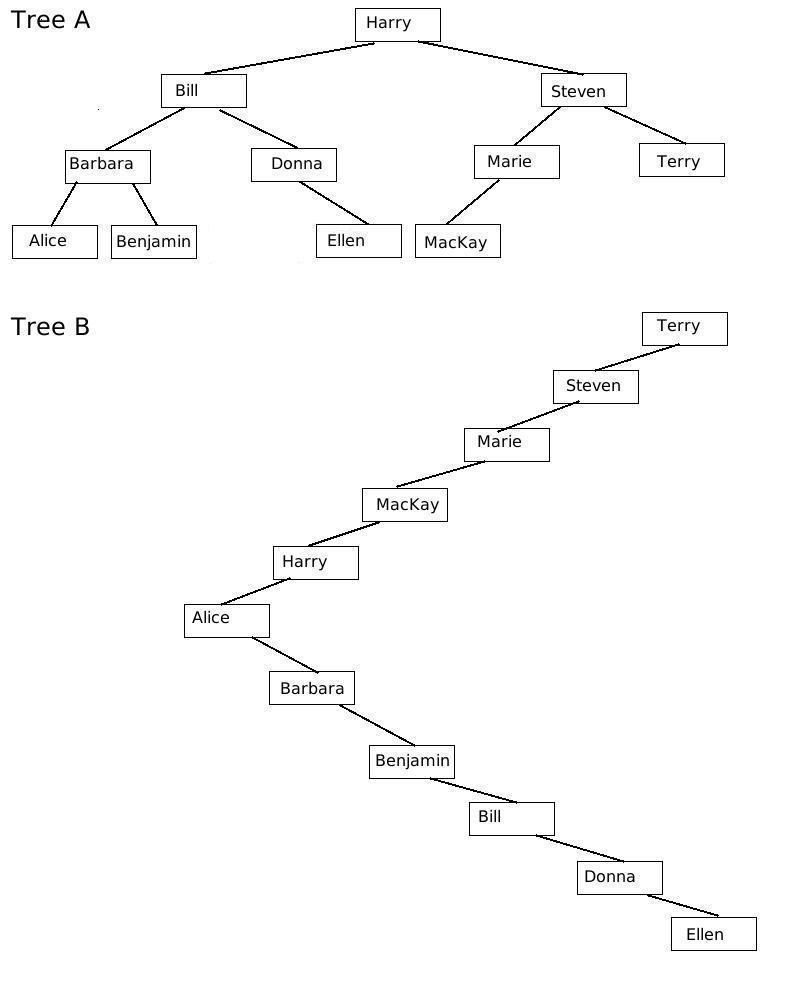
   1. Suppose that these trees were constructed using the simple insertion algorithm. Find an ordering of input data that would result in these trees.
   2. In Tree A, Harry is located in the root, while in Tree B Harry is shown about halfway down the tree. Find an ordering of data that also produces a list-like tree structure, where Harry is located at the far end of the list.
   3. Using your experience in parts a and b, consider any set of n pieces of data d₁, d₂, d₃, ..., d_n, and suppose d₁ < d₂ < d₃ < ... < d_n. Describe how you could order the inputted data, so that the resulting tree would be a linear-looking structure with d_j at the end.

   This exercise demonstrates that simple insertion can produce a list-like structure for any data set for at least one ordering of the input data.

2. Is the operation of deletion in a binary search tree "commutative" in the sense that deleting x and then y from a binary search tree leaves the same tree as deleting y and then x? Argue why it is or give a counter example.

3. Argue that since sorting n elements takes Ω(n lg n) time in the worse case in the comparison model, any comparison-based algorithm for constructing a binary search tree from an arbitrary list of n elements takes at least Ω(n lg n) time in the worse case.

4. Dale/Walker, Chapter 9, Problem 15a
   Show the final result after each letter is added.

5. Dale/Walker, Chapter 9, Problem 16a
   Show the final result after each number is added.

created January 4, 2022 revised January 4, 2022
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.

Copyright © 2011-2022 by Henry M. Walker. Selected materials copyright by Marge Coahran, Samuel A. Rebelsky, John David Stone, and Henry Walker and used by permission. This page and other materials developed for this course are under development. This and all laboratory exercises for this course are licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 International License.