CS 415: Algorithm Analysis

Some Definitions

A general tree is defined recursively as follows:

A null tree (or null list) is a tree.
If I is a data element and if T₁, T₂, T₃, ..., T_n are n trees, then

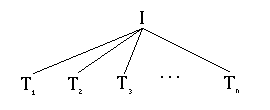
is also a tree.

Terminology

I is called the root or root node, and each T_i is called a subtree of the tree. Nodes that have only null subtrees are called leaves or leaf nodes.

Since this definition is recursive, it may be applied multiple times to construct more complex trees, such as the one shown below:

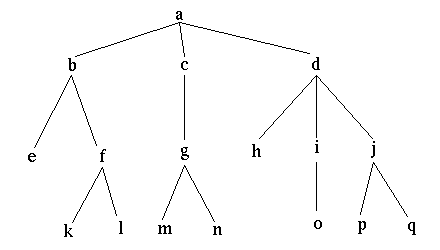
In this example, e, k, l, m, n, h, o, p, and q are leaves (or trees with null subtrees); a is the root of the overall tree. f is the root of a tree with k and l as subtrees, etc. Similarly, b is the root of a tree with two subtrees, one containing e and one containing f, k, and l.

Binary Search Trees

A binary search tree or BST is a special type of tree, in which

each node has at most a left and a right subtree
for each node, all values in the left subtree come before the value in the root, and
for each node, all values in the right subtree come after the value in the root.

A schematic view of such a tree follows:

Implementing Binary Search Trees in C++

The implementation of a binary search tree in C++ involves three structural components:

data elements: individual units of information
nodes: building blocks of a tree
an entire tree: the full collection of logical nodes

The following discussion examines each of these levels in some detail.

Data Elements: sn `Entry` Class

Binary search trees provide a flexible and rather efficient structure for organizing and retrieving ordered data. For generality, it is convenient to collect the desired data into an Entry class. Consistent with many applications, this class likely requires the following methods (as a minimum):

A constructor to create data element objects
Comparison operators (==, !=, <, <'=, >, >=)
A method to retrieve storeded data (e.g., a toString and/or an overloading of cout <<) to allow printing of data elements.

Example: A Campus Directory

To illustrate the use of data elements within a binary search tree, consider the application of developing a campus directory that contains both students and faculty. In this context, directory information might be stored in the Entry class with two subclasses, Student and Faculty:

This class hierarchy allows students and faculty to be intermixed within the campus directory.

Class `Entry` and two Subclasses `Student` and `Faculty`

To highlight principles of abstraction and unit testing, the Entry Class and its subclasses are defined in three files:

Class	Header File	Implementation File	Testing file
Entry	Entry.h	Entry.cpp	EntryTest.cpp
Student	Student.h	Student.cpp	StudentTest.cpp
Faculty	Faculty.h	Faculty.cpp	FacultyTest.cpp

With this organization,

each header file provides function prototypes that can be imported into other classes,
each implementation file can be compiled to an object file; a sample command-line statement would be
```
      g++ -c Entry.cpp
    
```
each test file can be compiled, linked with the object file, and run: a sample command-line statement sequence would be
```
      g++ EntryTest.cpp Entry.o -o EntryTest
      ./EntryTest
    
```
With this approach, these data element files can be written, compiled, and debugged separately. Further, once completed, the object files can be used for later work, without the need for further compiling.

Nodes in a tree: the `TreeNode` Class

For a binary search tree (or any binary tree, for that matter), each node will contain data, and each node will have a left and right field to designate addresses of the relevant subtrees — although either or both of the subtrees could be null. Thus, a TreeNode should have fields data, left, and right, together with constructors and methods to access and modify these fields.

In addition, binary search trees require that nodes conform to a special ordering — all nodes in a left subtree must have data smaller than in a root node, while all nodes in a right subtree must have larger (or equal) data. In order to maintain this property throughout the tree, we must be able to test the relative ordering of data. In C++, as noted above, we determine this ordering by overloading the relational operators for objects of the Entry class and its subclasses.

Class `TreeNode`

Class TreeNode illustrates a typical declaration for such a node class. In this case, good design dictates that this class be written to work with any type of data element (as long as the data can be created, compared, and printed). This desire for generality/flexibility has several conceptual and practical consequences.

Class TreeNode is a templated class, so a class parameter can be inserted when the class is included in an application.
Because details of the underlying compiled code depend upon the data element being included, this code cannot be compiled to a generic object file —different compiled object files are needed for each included data type. (See https://cplusplus.com/forum/general/12575/ for further details.)
Such compiling considerations in C++ motivate placing both header and implementation code in the same file. This yields a complete file for TreeNode.h.

A Binary Search Tree Class

A binary search tree (BST) provides a flexible and reasonably efficient structure for the storage and retrieval of data. In a university directory application, a user would search a directory by name, and a successful search would return additional information about the individual.

Before implementing any class, we must identify the appropriate operations. Some common operations for a Binary Search Tree class include:

construct a tree,
add an entry,
retrieve an entry, given the name,
update an entry,
print all entries (alphabetically by name), and
remove an entry.

In the following discussion, we outline an algorithm for several of these operations, sometimes describing an iterative approach and sometimes using recursion; often either iteration or recursion could be used for these operations.

For our implementation, we also need an image of how a BSTree class will package tree information. Here, various tree nodes to point to their subtrees within the BSTree. Thus, the BSTree class itself only need specify the initial node or root. As an example, the following diagram shows a binary search tree, annotated to show the data type of various components.

A `BSTree` Class, with Commentary

Class BSTree implements a binary search tree, including several methods already identified.

The reader is encouraged to review various elements of the code in conjunction with the following commentary on the various methods.

Constructor

As with lists, an initial binary search tree will be empty. This may be implemented by setting the root field to null.

`lookup`

Searching in a binary search tree proceeds downward from the root, following a reasonably common recursive pattern.

Base Case 1: The desired item is found and can be returned.
Base Case 2: A null is encountered at the bottom of the tree. With nothing more to search, the search can report the item is not found.
Recursive Case 1: The desired item comes after the item in the current node, and the search should continue in the right subtree.
Recursive Case 2: The desired item comes before the item in the current node, and the search should continue in the left subtree.

`lookup`'s return type

The idea of the lookup method is to take a data element as a parameter and to return that data element. However, at a detail level, a question within C++ arises as to whether the parameter and the return type should be an object or a pointer to the object. Both could work, leading to several design issues.

parameter type: If the lookup method passes an object, then the object may need to be copied with each call. For efficiency, passing a pointer is more efficient.
return type: If the lookup method returns an object, then C-based processing often takes one of two approaches.
- Some designated object could be identified as a "not found" result. However, this approach The data would requires construction of a new object, which subsequently would need to be deallocated, and care would be needed to avoid a memory leak.
- An "error" parameter could be included in the lookup signature, and this parameter would have to be checked consistently after each call. While possible, this approach often complicates processing.
If the lookup method returns an address, then the result would be either a pointer to a data element or a null value. Including the call within a conditional statement allows simple checking:
```
      Entry ptr;
      if ((ptr = lookup (---)) == NULL) {
          // not found
      } else P
          // found
      {
      
```

`print`

A recursive algorithm starts at the root and applies the following steps for each node:

print the node's left subtree,
print the data at the node,
print the node's right subtree.

The above sequence of events is called an in-order traversal of a tree. Similarly, printing the data at the node, then the left subtree, and then the right subtree is called a pre-order traversal. Printing the data in the node last gives a post-order traversal.

`insert`

For variety, we use an iterative approach to insert entries into a tree. To start, a simple base case checks whether the tree is empty. If so, a new node is generated, initialized with the relevant data, and identified as the new root.

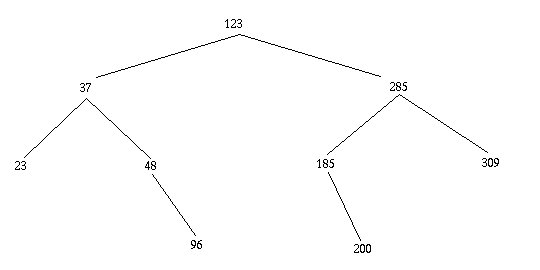
To understand the rest of the insertion process, consider the insertion of the number 153 into the following tree (which repeats the tree given above).

To insert 153, we start at the top of the tree. Checking that 153 comes after the value in the root (123), we advance to the right subtree. We now check that 153 comes before 285, so we advance to the left subtree of 285. Again, we compare 153 with value 185, and realize we should move left. Here, however, we discover there are no further nodes. Thus, we create a new node, place 153 in that node, and identify the new node as the left child of 185's node.

In the code for insert, the variable ptr keeps track of where we are as we work downward node-by-node from the root. To test if an item (newEntry for the BSTree code) comes before the value in a node, we use the following sequence:

ptr identifies a given node, so
ptr.getData() identifies an entry at that node. Also,
newEntry specifies the new data to add, so
newEntry.compareTo is a method to compare data. Thus,
newEntry.compareTo(ptr.getData()) uses the comparison method to compare the information for the new newEntry with the information for the node ptr.getData().

Testing

The complete directory program DirectoryBST.cpp combines all of the classes discussed in this reading (Entry, Student, Faculty, TreeNode, and )BSTree).

For convenience, all files within this example are packaged together in the compressed file tree-package.tgz.

Running `BSTree`

Although individual files identified in this reading could be downloaded and stored separately, these files are compressed into a single file, trees-package.tgz. After downloading this file, unpack it with the command

  tar -xvf tree-package.tgz

Since compiling the complete program requires creating object files for the Entry and its subclasses, as well as handling the templated classes (TreeNode and BSTree) and the application DirectoryBST, the variou> completion steps are organized into a Makefile—also included in the compressed file. After decompressing all files, move the newly created directory and type

  make DiretoryBST

When completion has completed, run the test program with the command

  ./DirectoryBST

CS 415, Section 002	Sonoma State University	Spring, 2022

Algorithm Analysis
Instructor: Henry M. Walker Lecturer, Sonoma State University Professor Emeritus of Computer Science and Mathematics, Grinnell College

Reading: Tree Basics

Summary

Some Definitions

Terminology

Binary Search Trees

Implementing Binary Search Trees in C++

Data Elements: sn `Entry` Class

Example: A Campus Directory

Class `Entry` and two Subclasses `Student` and `Faculty`

Nodes in a tree: the `TreeNode` Class

Class `TreeNode`

A Binary Search Tree Class

A `BSTree` Class, with Commentary

Class `BSTree`

Constructor

`lookup`

`lookup`'s return type

`print`

`insert`

Testing

Running `BSTree`

created 18 April 2000 revised 24 March 2005 revised 5 April 2012 modest editing 22 April 2012 translated from Java to C++ January 2021
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.

Reading: Tree Basics

Summary

Some Definitions

Terminology

Binary Search Trees

Implementing Binary Search Trees in C++

Data Elements: sn Entry Class

Example: A Campus Directory

Class Entry and two Subclasses Student and Faculty

Nodes in a tree: the TreeNode Class

Class TreeNode

A Binary Search Tree Class

A BSTree Class, with Commentary

Class BSTree

Constructor

lookup

lookup's return type

print

insert

Testing

Running BSTree

Data Elements: sn `Entry` Class

Class `Entry` and two Subclasses `Student` and `Faculty`

Nodes in a tree: the `TreeNode` Class

Class `TreeNode`

A `BSTree` Class, with Commentary

Class `BSTree`

`lookup`

`lookup`'s return type

`print`

`insert`

Running `BSTree`