CS 415: Algorithm Analysis

Computablity and Unsolvability

The Halting Problem is said to be "unsolvable".

Outline the basic argument that shows that the Halting Problem is unsolvable.
How is being "unsolvable" different from stating that we have not yet found an algorithm that solves the problem?

A company believes there would be a strong market for a software package that would take the specifications of a problem and the code for a program as input and would prove whether the program meets its specifications in all cases. That is, the software package would prove whether or not a program always meets its specifications.

Although the prospect of such software package might capture one's imagination, such can package cannot be successfully produced. Explain why an error-free version of this software is impossible to develop.

Consider the concepts of a NP-Hard problem and an NP-Complete problem.

Can a problem be NP-Hard without being NP-Complete? Explain.
Can a problem be NP-Complete without being NP-Hard? Explain.

Compounding of Numeric Error

Suppose a loop is to start at a value start and finish at (or near) a value end in about n+1 iterations, with iterations increasing by a value increment = (end-start)/n each time.

Two loop structures are proposed:

      // approach 1
      increment = (end - start)/n;
      for (i = 0; i <= n; i++){
           value = start + i * increment;              
          /* processing for value */
        }

      // approach 2
      value = start;
      increment = (end - start)/n;
      while (value <= end) {
         /* processing for value */
         value += increment;             
      }

Although the first approach requires somewhat more arithmetic within the loop than the second, it likely will provide better accuracy. Identify two distinct reasons why the first approach should be preferred over the second.

Suppose y = f(x) is a function that decreases from x=a to x=b, on the interval [a, b], with a<b.

Throughout this interval, assume f(x)>0, and assume the Trapezoidal Rule were to be used to approximate the area under y = f(x) on the interval [a, b].

Should the main loop begin at start and go toward end or begin at end and go toward start, or is either order fine? Explain.
Write the code that implements the Trapezoidal Rule for this function on this interval.

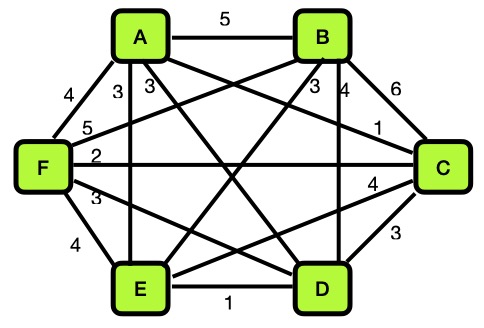
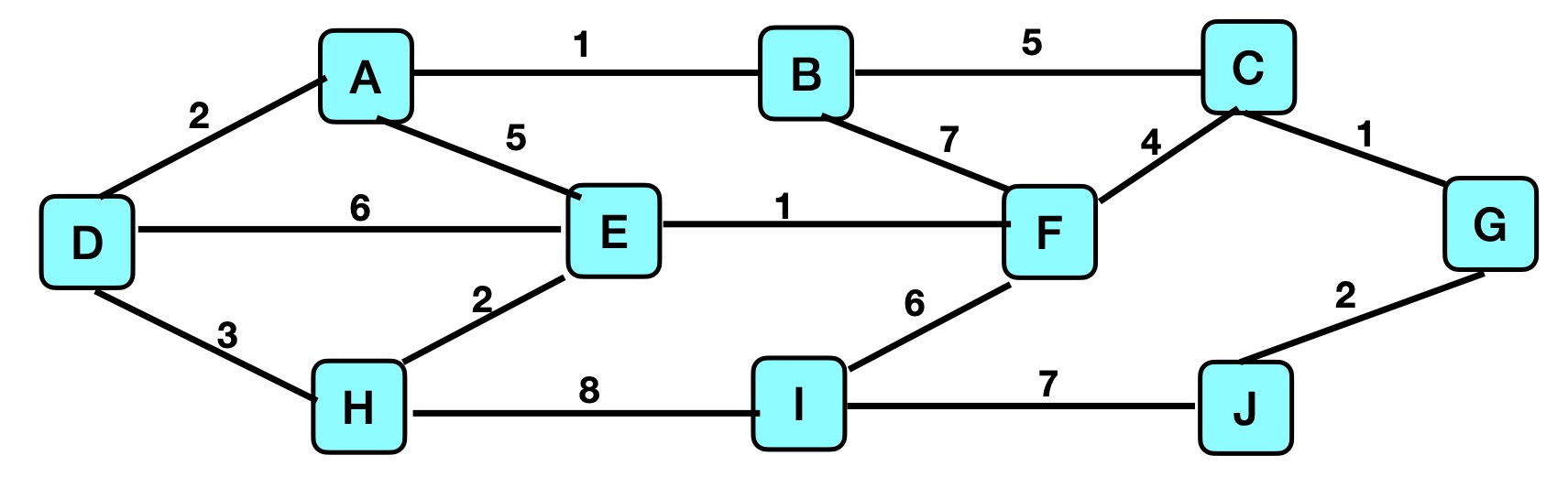
Approximation Algorithms for the Traveling Salesperson Problem

Pages 438-440 of the textbook describe how to use a Branch-and-Bound algorithm to find an approximate solution to the Traveling Salesperson Problem, and pages 444-448 describe a "Twice-around-the-tree" algorithm that uses a different approach to approximate another solution.

Apply each of these algorithms to find approximate solutions to the Traveling Salesperson Problem for each of the following graphs.

In each case, if the graph does not meet the required assumptions for an algorithm, indicate what condition(s) is(are) violated, rather than applying the algorithm.

Graph A
Graph B

Approximation Algorithms for Roots of a Function

Suppose we are given a continuous function f, and we want to approximate a value r where f(r)=0. (Jargon: r is called a root of the function f.)

Work with these numeric methods requires you to graph functions, so that you have a visual representation of a function's graph. For this purpose, you can use any graphing software that you like. One option is Graph a function from desmos.com.

The Bisection Method

The following question is based on the Reading on the Bisection Method.

Write a program that uses the Bisection Method to approximate a root of a function.
- The start of the program should define a function
```
double f (double x)
```
  for which the program is to find a root.
- The program should define a new function
```
double find_root (double a, double b, double accuracy)
```
  which works as follows:
  - find_root should use an assert statement to check that f(a) and f(b) have different signs. (The program should terminate if this assumption is not met.)
  - Another assert statement at the beginning of find_root should check that the accuracy is positive.
  - find_root should continue to cut the interval in half, following the Bisection Method, until either f(m)=0 for a computed midpoint m or the newly computed interval is shorter than the accuracy specified.
  - find_root should return the computed midpoint of the final interval.
- The main program should ask the user to enter endpoints a and b and the accuracy. The main program then should call find_roots with the appropriate parameters and report the result.

Newton's Method

Consult Levitin's textbook, Section 11.4 for details on Newton's Method, including the main formula.

CS 415, Section 001	Sonoma State University	Fall, 2022

Algorithm Analysis
Instructor: Henry M. Walker Lecturer, Sonoma State University Professor Emeritus of Computer Science and Mathematics, Grinnell College