CS 415, Section 001 Sonoma State University Fall, 2022
 
Algorithm Analysis
Instructor: Henry M. Walker

Lecturer, Sonoma State University
Professor Emeritus of Computer Science and Mathematics, Grinnell College

Although much of this course is well developed, some details can be expected to evolve as the semester progresses.
Any changes in course details will be announced promptly during class.

Worksheet on Greedy Algorithms

Huffman Trees and Codes

  1. Huffman Algorithm

    1. Construct a Huffman tree from the following set of frequencies. (Always put the smaller subtree to the left. If there is a tie, put the leaf to the left.)

      a   b   c   e   g   i   j   o   m   n   p   r   s   t   u   <space>
      2 1 4 4 1 2 1 1 1 1 1 2 3 3 2 5
    2. Using your tree in Part a, encode the message "computer science is a great subject".

  2. Construct a Huffmantree from the following set of frequencies.
    a   r   i   e   o   u   s   t  
    5 2 4 6 3 1 7 8

  3. Decode the front of the AP Computer Science t-shirt for 2002.

Minimum Cost Spanning Trees

  1. Consider the following undirected graph:

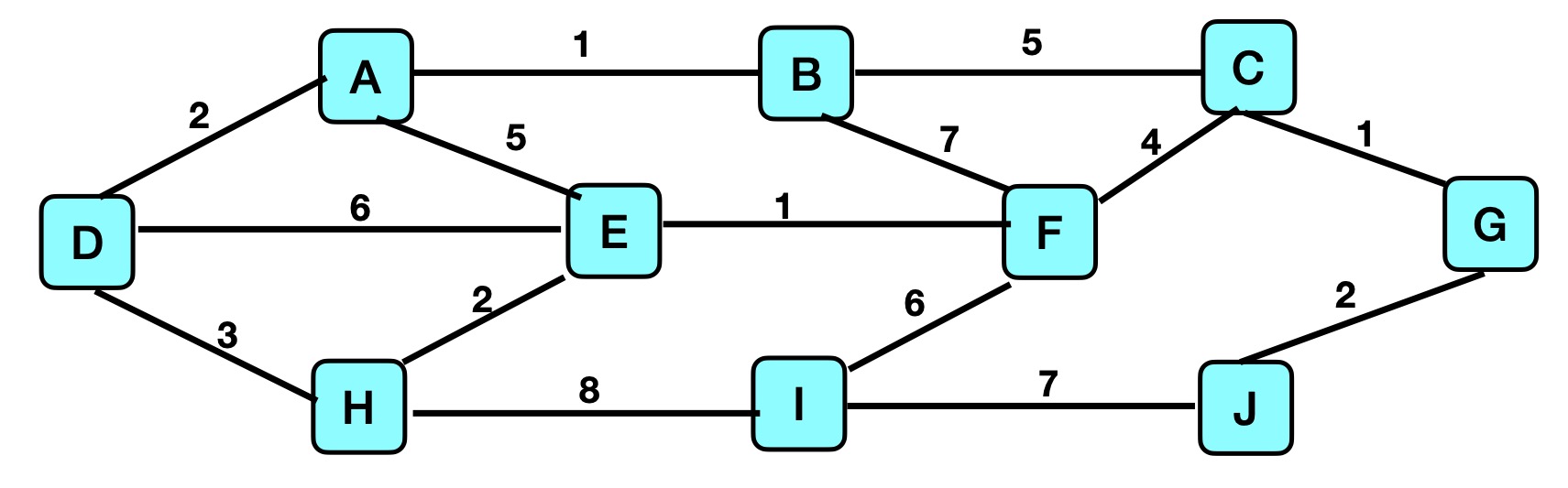
    undirected graph

    1. Find the shortest paths from vertex C to all other vertices.

    2. Find the minimum cost spanning tree, showing the main steps in applying the algorithm.

  2. Repeat the previous problem for the following graph.

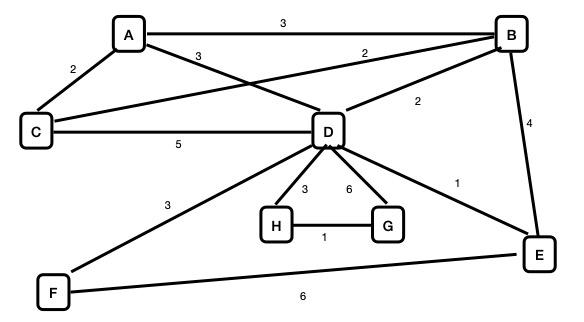
    undirected graph

  3. Given an undirected graph, a minimum cost spanning trees need not be unique. Given an example of a graph with two different minimum cost spanning trees, where the graph has the fewest number of vertices and the fewest number of edges. In addition to displaying the graph and the two different minimum cost spanning trees, provide an explanation as to why this graph is the smallest possible with two different such trees.

created April 25, 2022
revised April 25, 2022
revised July 24, 2022 		Valid HTML 4.01! Valid CSS!
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.
ccbyncsa.png

Copyright © 2011-2022 by Henry M. Walker.
Selected materials copyright by Marge Coahran, Samuel A. Rebelsky, John David Stone, and Henry Walker and used by permission.
This page and other materials developed for this course are under development.
This and all laboratory exercises for this course are licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 International License.