Worksheet on Graph Representations, Graph Traversals, and Heaps

This worksheet/lab is in two parts: graphs and heaps.

Graphs

This section in graphs contains exercises on

• graphs specified by adjacency matrices,
• graphs specified by sets, and
• graph analysis.

Adjacency Matrices and Lists

1. Consider the following adjacency matrix S for a weighted, directed graph. (Note: 0 means there is no edge.)

   	A	B	C	D	E	F	G
   A	0	10	6	4	0	7	0
   B	10	0	9	0	11	0	18
   C	6	9	0	1	1	0	0
   D	4	0	1	0	1	2	0
   E	0	11	1	1	0	0	14
   F	7	0	0	2	0	0	15
   G	0	18	0	0	14	15	0

   1. Draw a picture of the graph represented by this adjacency matrix S without the weights.

   2. Can this graph be considered as a directed graph? As an undirected graph? Explain.

   3. List the vertices in depth-first order beginning with vertex A. When you have a choice in processing vertices, pick them in alphabetical order; that is, when working with a stack and more than one vertex may be selected, push the vertices onto the stack in alphabetical order.

   4. List the vertices in breadth-first order beginning with vertex A. Again, when you have a choice among vertices, pick them in alphabetical order; that is, when working with a queue and more than one vertex may be selected, enqueue the vertices onto the stack in alphabetical order.

2. Next, consider the graph with the following adjacency matrix.

   	A	B	C	D	E	F	G
   A	0	10	6	4	0	7	0
   B	0	0	9	0	11	0	18
   C	6	9	0	1	1	0	0
   D	4	0	1	0	1	2	0
   E	0	0	1	1	0	0	14
   F	7	0	0	2	0	0	15
   G	0	18	0	0	0	0	0

   1. Draw a picture of the graph represented by this adjacency matrix S without the weights.

   2. Is the graph directed or undirected? Explain.

   3. List the vertices in depth-first order beginning with Vertex A. When there is a choice, process the vertices and edges from left to right.

   4. List the vertices in breadth-first order beginning with Vertex A. Again, when there is a choice, process the vertices and edges from left to right.

A Graph Specified by Sets

3. Consider the following graph.

   • G = {V,E}
   • V = {A, B, C, D, E, F,G, H}
   • E = {<A, B >, <A, C >, <A, D >, <B, H >, <F, E >, <F. H >, <H, E >, <F, C >, <C, F >, <D, F >, }

   1. Write the adjacency matrix for this graph, based upon the alphabetical ordering of the vertices given.

   2. Draw the adjacency list representation for this graph.

Analytical/Structural Results

4. Write a careful analysis for the following.

   1. Suppose a connected graph has v vertices and e edges. What is the complexity of a depth-first search?

      1. Assume the queue is implemented with an array, and the graph by an adjacency matrix.

      2. Assume the queue is implemented with a linked list, and the graph with adjacency lists.

   2. A claim is made that a complete directed graph of n vertices has n(n-1) edges, while a complete undirected graph of n vertices has n(n-1)/2 edges. Is this claim true? If so outline a proof. If not, give a counter example.

      Hint: You could use an argument related to permutations and combinations from Discrete Mathematics (e.g., CS 242).

Heaps

This section is divided into

• discussion,
• 0-based indexing of nodes,
• insertion into a heap",
• deletion from a heap", and
• construction of a heap within an array

Discussion

A max-heap is a binary tree with the property that the value at each node is larger (according to some ordering) than the values stored in either child. Similarly, a min-heap is a binary tree with the property that the value at each node is smaller (according to some ordering) than the values stored in either child.

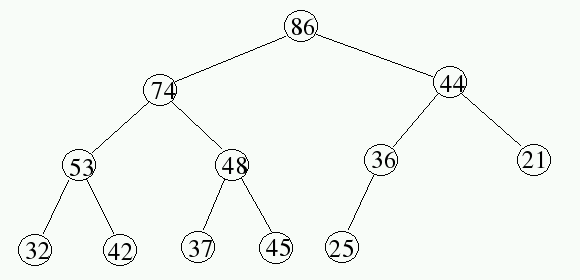
Further, we restrict our attention to trees which are completely balanced. All nodes have 2 children, except at the bottom of the tree. The last row of the tree may not be full, but any items on the last level are moved left as much as possible. For example, the following tree illustrates the shape of a tree and the ordering of values within the tree for a max-heap.

A Simple Labeling of Nodes

To identify the nodes in a tree, the simplest approach is to number the nodes level-by-level from the root downward. Within a level, nodes are numbered left to right. Also, for simplicity, many textbooks assign the index 1 to the root node.

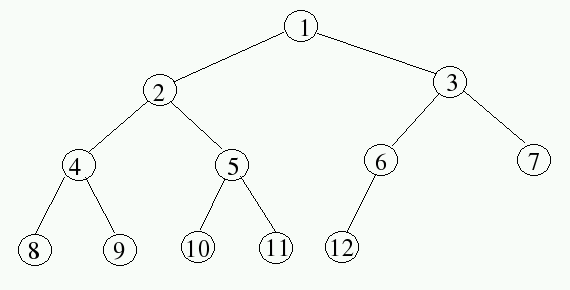
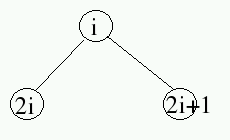
In examining the label nodes, a pattern emerges: for each node labeled i, the left child has label 2*i and the right node has label 2*i+1.

Note: As previously noted, some textbooks, such as Data Structures and Problem Solving Using Java, Fourth Edition by Mark Allen Weiss. uses this numbering scheme in writing code, with the top node numbered 1. If one considers an array element 0, Weiss suggests filling that position with -∞ for a min-heap or ∞ for a max-heap.

0-based Labeling of Nodes

If we start labeling at 0 rather than 1, the labeling of nodes becomes:

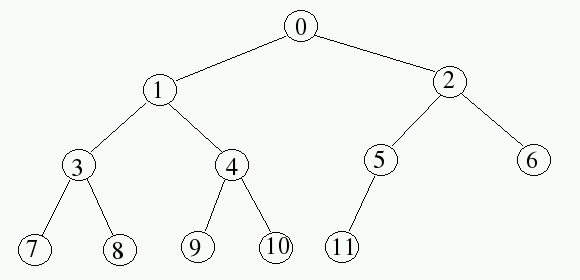
5. In the context of 0-based labeling, identify a pattern for moving from a node with label j to its left child and its right child. What labels would be found on the left and right nodes of a node with label j?

Connecting a Heap with an Array

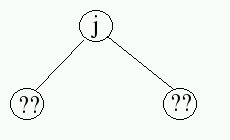
Since nodes in a heap fit a straight forward identification system, there is a natural mapping between the logical nodes in a heap and the indexed elements of an array.

Insertion into a Heap

In class we considered how to insert an item into a heap and maintain the structure. In each case, we first place the item at the end of a tree (as far left as possible in the last row). The item then is worked up from its position, until the data in the tree are appropriately ordered.

6. The following heap repeats the structure given at the beginning of this lab:

   

   Using this structure as a start, insert the values 30, 25, 55, 81, and 95. Show the structure of the tree and the values in each node after each insertion.

Deletion from a Heap

In class, we also considered how to remove the top-priority item from a heap: remove the root as the item to be returned, move the last item from the end of the heap to the root, and work that item down in the heap until the data are properly ordered.

7. Starting with the original heap from step 2, remove four items in sequence. Show the structure of the tree and the values in each node after each deletion.

Constructing a Heap within an Array

In class, we discussed starting with an array of data and working from the bottom toward the top to rearrange the data to yield a heap. For Steps 4 and 5, consider working with a min-heap.

8. In the following questions, consider a heap implemented with 0-based indexing.

   1. Suppose an array of twelve elements, a[12], is initialized with a[i] = 20-i for each i. What rearrangements, if any, need to be done in order to make the corresponding tree structure into a heap? Show the data in the array once a heap is achieved.

   2. Suppose the array of twelve elements, a[12], is initialized with a[i] = i for each i. What rearrangements, if any, need to be done in order to make the corresponding tree structure into a heap? Show the data in the array once a heap is achieved.

created December 1, 2018 revised December 2, 2018 revised December 27-30, 2021 revised February 4, 2022 reformatted and heap material added July 28, 2022
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.

Copyright © 2011-2022 by Henry M. Walker. Selected materials copyright by Marge Coahran, Samuel A. Rebelsky, John David Stone, and Henry Walker and used by permission. This page and other materials developed for this course are under development. This and all laboratory exercises for this course are licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 International License.