Worksheet on Graph Basics and Singly-nested Loop Invariants
Work for this worksheet falls into two groups:
Graph Basics
Adjacency Matrices and Lists
-
Consider the following adjacency matrix S for a weighted, directed
graph. (Note: 0 means there is no edge.)
| | A | B | C
| D | E | F | G
|
| A | 0 | 10 | 6 | 4 | 0 | 7 | 0
|
| B | 0 | 0 | 9 | 0 | 11 | 0 | 18
|
| C | 6 | 9 | 0 | 1 | 1 | 0 | 0
|
| D | 4 | 0 | 1 | 0 | 1 | 2 | 0
|
| E | 0 | 0 | 1 | 1 | 0 | 0 | 14
|
| F | 7 | 0 | 0 | 2 | 0 | 0 | 15
|
| G | 0 | 18 | 0 | 0 | 0 | 0 | 0
|
-
Draw a picture of the graph represented by this adjacency matrix S without
the weights.
-
Can this graph be interpreted as being directed? Explain.
-
Can this graph be interpreted as being undirected? Explain.
-
List the vertices in depth-first order beginning with vertex A. When
you have a choice among vertices, pick them in alphabetical order.
-
List the vertices in breadth-first order beginning with vertex A.
Again, when you have a choice among vertices, pick them in
alphabetical order.
A graph Specified by Sets
-
Consider the following graph, specified in terms of sets of
vertices and edges.
- G = {V,E}
- V = {A, B, C, D, E, F, G, H}
- E = {<A, B >, <A, C >, <A, D >, <B, H
>, <F, E >, <F. H >, <H, E >, <F, C >,
<C, F >, <D, F >, }
-
Write the adjacency matrix for this graph, based upon the
alphabetical ordering of the vertices given.
-
Draw the adjacency list representation for this graph.
-
List the vertices in depth-first order beginning with vertex A. When
you have a choice among vertices, pick them in alphabetical order.
-
List the vertices in breadth-first order beginning with vertex A.
Again, when you have a choice among vertices, pick them in
alphabetical order.
Analytical/Structual Results
-
Suppose a connected graph has v vertices and e edges. What is the complexity of
a depth-first search?
-
Assume the queue is implemented with an array, and the graph by an
adjacency matrix.
-
Assume the queue is implemented with a linked list, and the graph with
adjacency lists.
Invariants for Singly-nested Loops
In this section, you are asked to write three programs, all
involving loop invariants for singly-nested loops.
Binary Search Algorithms
-
The Reading
Introduction to Loop Invariants discusses two implementations
of a binary search, based on different loop invariants, and
program binary-searches.c
provides the full code for each of these invariants, as well as a
framework for testing these functions.
Expand binary-searches.c to include a new
function search3 that implements and tests a binary
search that uses the following loop invariant.
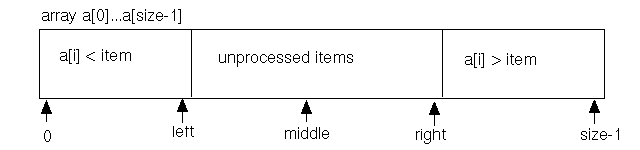
That is,
left is the largest array index for which it is
known that a[left] < item (provided some
elements are known to be less than item, or equivalently
left is the first index for
which a[left+1] is unprocessed (provided some
elements have not yet been examined).
right is the largest array index for
which a[right] is unprocessed (provided some
elements have not yet been examined), or equivalently
right is the first index .for which it is
known that a[right+1] > item (provided some
elements are known to be larger than item
The Dutch National Flag Problem
The Dutch National Flag Problem was first proposed by W.H.J. Feijen and
made famous by Edsger W. Dijkstra. The following formulation relates the
problem to arrays in C.
Enumerations in C are described in Kernighan and Ritchie, Section 2.3,
page 39. For example, an enumeration with three colors could be declared
as:
enum color { red, white, blue };
and we may consider an array of colors:
#define size 50 /* number of elements in an array */
color colors [size];

When we begin, we do not know the number of elements of each color, and we
are not even assured that each color is actually present.
The Dutch National Flag Problem seeks to sort this array, so that red's
come first, then white's, and then blue's. Movement of array elements may
be accomplished only by swapping two items.

Solution
Although one approach to this problem involves simple sorting (just
consider red < white < blue), the problem can be solved in a single
pass of the data. The idea is to identify an array diagram that describes
sections of colors as loop invariants. Writing the code then is reasonably
straightforward; we just have to maintain the invariant!
For this problem, at least four different pictorial loop invariants
initially come to mind:

In each case, we must introduce variables to keep track of the edge of the
red, white, and blue sections. Initially, these sections contain no
elements, and the entire array is unprocessed. Then as processing
proceeds, the program looks at successive unprocessed elements and puts
them in their correct locations — maintaining the loop invariant.
-
For two of these pictorial loop invariants, introduce
variables to record the index of a boundary between colors, and
describe the invariant carefully in words. Then add the
variables to the pictorial loop invariants.
Once the loop invariants are described, you are to create two loop
segments to solve the Dutch National Flag Problem,using the identified
invariants.
-
For each of the two approaches, initialize your variables, so that the
pictorial loop invariants are satisfied at the start of processing.
-
Complete the loop processing, maintaining the identified loop invariant.
-
For this problem, you are encouraged to write a complete program, so
you can test that your code works properly. However, submitting just
the code for the two procedures is adequate.




