CS 415, Section 001	Sonoma State University	Fall, 2022

Algorithm Analysis
Instructor: Henry M. Walker Lecturer, Sonoma State University Professor Emeritus of Computer Science and Mathematics, Grinnell College

Although much of this course is well developed, some details can be expected to evolve as the semester progresses.
Any changes in course details will be announced promptly during class.

Reading on the Bisection Method

Suppose we are given a continuous function f, and we want to approximate a value r where f(r)=0. (Jargon: r is called a root of the function f.) While finding r can be a difficult problem in general, suppose that we can guess two points a and b (perhaps from a graph) where f(a) and f(b) have opposite signs. If the graph crosses the x-axis at the midpoint m of the interval between a and b (i.e., if f(m)=0), then m is the desired root of the function. Otherwise, the four possible cases are shown below:

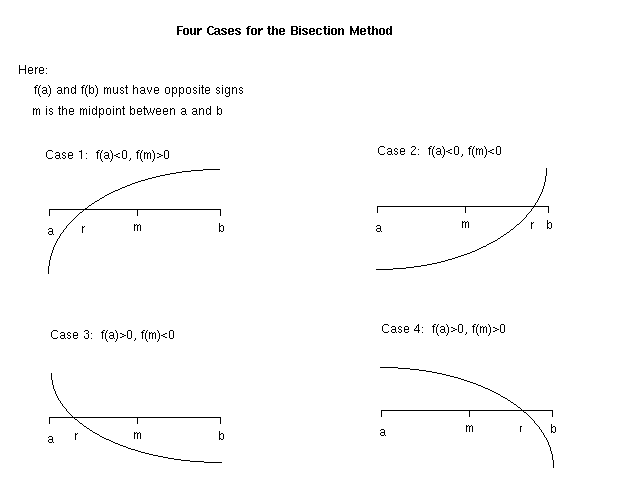
Since this setting assumes we are given a and b for which f(a) and f(b) have opposite signs, we can infer that a root r must lie in the interval [a, b]. In one step, we can cut this interval in half as follows. If f(a) and f(m) have opposite signs, then r must lie in the interval [a, m]; otherwise, r must lie in the interval [m, b].

One simple way to determine if two numbers have the same sign is to compute their product. If the product is positive, the two numbers are both positive or both negative. If the product is negative, one of the original numbers is positive and the other is negative.

Following this process of cutting the interval in half, we can continue until the interval is very narrow. At this stage, the midpoint of the interval will be a reasonable approximation to a root of the function.

created July 25, 2022 revised July 25, 2022
For more information, please contact Henry M. Walker at walker@cs.grinnell.edu.